
ЁОЬтФПЁПЫцзХЕчзгВњЦЗЕФВЛЖЯИќаТЭъЩЦЃЌИќЖрЕФЕчзгВњЦЗж№ВНзпШыДѓМвЕФЪРНчЃЌИјДѓМвДјРДСЫЗсИЛЖрВЪЕФЩњЛюЃЌЕЋвВДјРДСЫвЛаЉИКУцЕФгАЯьЃЌФГЙЋЫОЫцМДГщШЁ![]() ШЫЖдФГЕчзгВњЦЗЪЧЗёЖдШеГЃЩњЛюгавцНјааСЫЮЪОэЕїВщЃЌВЂЖдВЮгыЕїВщЕФ
ШЫЖдФГЕчзгВњЦЗЪЧЗёЖдШеГЃЩњЛюгавцНјааСЫЮЪОэЕїВщЃЌВЂЖдВЮгыЕїВщЕФ![]() ШЫжаЕФФъСфВуДЮвдМАвтМћНјааСЫЗжРрЃЌЕУЕНЕФЪ§ОнШчЯТБэЫљЪОЃК
ШЫжаЕФФъСфВуДЮвдМАвтМћНјааСЫЗжРрЃЌЕУЕНЕФЪ§ОнШчЯТБэЫљЪОЃК
|
| змМЦ | |
ШЯЮЊФГЕчзгВњЦЗЖдЩњЛюгавц |
|
|
|
ШЯЮЊФГЕчзгВњЦЗЖдЩњЛюЮовц |
|
|
|
змМЦ |
|
|
|
ЃЈ1ЃЉИљОнБэжаЕФЪ§ОнЃЌФмЗёдкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌШЯЮЊЕчзгВњЦЗЕФЬЌЖШгыФъСфгаЙиЯЕЃП
ЕФЧАЬсЯТЃЌШЯЮЊЕчзгВњЦЗЕФЬЌЖШгыФъСфгаЙиЯЕЃП
ЃЈ2ЃЉЮЊСЫД№аЛВЮгыЮЪОэЕїВщЕФШЫдБЃЌИУЙЋЫОЖдВЮгыБОДЮЮЪОэЕїВщЕФШЫдБНјааГщНБЛюЖЏЃЌНБН№ЖювдМАЗЂЗХЕФИХТЪШчЯТЃК
НБН№Жю |
|
|
|
ИХТЪ |
|
|
|
ЯждкМзЁЂввСНШЫВЮгыСЫГщНБЛюЖЏЃЌМЧСНШЫЛёЕУЕФНБН№змН№ЖюЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ВЮгыЙЋЪНЃК 
СйНчжЕБэЃК
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнСаСЊБэЃЌМЦЫуЙлВтжЕ![]() ЃЌЭЈЙ§ЖдееЬтФПжаЕФЪ§жЕБэЃЌМДПЩЕУГіЭГМЦНсТлЃЎ
ЃЌЭЈЙ§ЖдееЬтФПжаЕФЪ§жЕБэЃЌМДПЩЕУГіЭГМЦНсТлЃЎ
ЃЈ2ЃЉ![]() ЕФПЩФмШЁжЕЮЊ
ЕФПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓГіЯргІИХТЪжЕЃЌЕУЕНЗжВМСа.ЧѓГіЪ§бЇЦкЭћ.
ЃЌЧѓГіЯргІИХТЪжЕЃЌЕУЕНЗжВМСа.ЧѓГіЪ§бЇЦкЭћ.
ЪдЬтНтЮіЃК
ЪдЬтНтЮіЃКЃЈ1ЃЉвРЬтвтЃЌдкБОДЮЕФЪЕбщжаЃЌ ![]() ЕФЙлВтжЕ
ЕФЙлВтжЕ![]()
![]() ЃЌ
ЃЌ
ЙЪПЩвддкЗИДэЮѓЕФИХТЪВЛГЌЙ§![]() ЕФЧАЬсЯТЃЌШЯЮЊЖдЕчзгВњЦЗЕФЬЌЖШгыФъСфгаЙиЯЕ.
ЕФЧАЬсЯТЃЌШЯЮЊЖдЕчзгВњЦЗЕФЬЌЖШгыФъСфгаЙиЯЕ.
ЃЈ2ЃЉ![]() ЕФПЩФмШЁжЕЮЊ
ЕФПЩФмШЁжЕЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ ![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
|
|
|
|
|
|
|
|
|
|
|
|
![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧ(ЁЁЁЁ)
A. ШєУќЬт![]() ЖМЪЧецУќЬт,дђУќЬтЁА
ЖМЪЧецУќЬт,дђУќЬтЁА![]() ЁБЮЊецУќЬт
ЁБЮЊецУќЬт
B. УќЬтЁА![]() ЁБЕФЗёЖЈЪЧЁА
ЁБЕФЗёЖЈЪЧЁА![]() ,
,![]() ЁБ
ЁБ
C. УќЬт:ЁАШє![]() ,дђ
,дђ![]() Лђ
Лђ![]() ЁБЕФЗёУќЬтЮЊЁАШє
ЁБЕФЗёУќЬтЮЊЁАШє![]() ,дђ
,дђ![]() Лђ
Лђ![]() ЁБ
ЁБ
D. ЁА![]() ЁБЪЧЁА
ЁБЪЧЁА![]() ЁБЕФБивЊВЛГфЗжЬѕМў
ЁБЕФБивЊВЛГфЗжЬѕМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈ1ЃЉСю![]() ЃЌЪдЬжТл
ЃЌЪдЬжТл![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШєЖд![]() КуГЩСЂ,Чѓ
КуГЩСЂ,Чѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩ![]() ЃЌЖдКЏЪ§ЧѓЕМЃЌбаОПЕМКЏЪ§ЕФе§ИКЕУЕНЕЅЕїадМДПЩЃЛЃЈ2ЃЉгЩЬѕМўПЩжЊ
ЃЌЖдКЏЪ§ЧѓЕМЃЌбаОПЕМКЏЪ§ЕФе§ИКЕУЕНЕЅЕїадМДПЩЃЛЃЈ2ЃЉгЩЬѕМўПЩжЊ![]() Жд
Жд![]() КуГЩСЂЃЌБфСПЗжРы
КуГЩСЂЃЌБфСПЗжРы![]() ЃЌСю
ЃЌСю![]() ЃЌЧѓетИіКЏЪ§ЕФзюжЕМДПЩ.
ЃЌЧѓетИіКЏЪ§ЕФзюжЕМДПЩ.
НтЮіЃК
ЃЈ1ЃЉгЩ![]() ЕУ
ЕУ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() КуГЩСЂЃЌдђ
КуГЩСЂЃЌдђ![]() ЕЅЕїЕнМѕЃЛ
ЕЅЕїЕнМѕЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ  ЃЌСю
ЃЌСю ЃЌ
ЃЌ
Сю .
.
злЩЯЃКЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЕЅЕїЕнМѕЃЌЮодіЧјМфЃЛ
ЕЅЕїЕнМѕЃЌЮодіЧјМфЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ  ЃЌ
ЃЌ 
ЃЈ2ЃЉгЩЬѕМўПЩжЊ![]() Жд
Жд![]() КуГЩСЂЃЌдђ
КуГЩСЂЃЌдђ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() Жд
Жд![]() КуГЩСЂ
КуГЩСЂ
ЕБ![]() ЪБЃЌгЩ
ЪБЃЌгЩ![]() ЕУ
ЕУ![]() .Сю
.Сю![]() дђ
дђ
 ,вђЮЊ
,вђЮЊ![]() ,Ыљвд
,Ыљвд![]() ,МД
,МД![]()
Ыљвд![]() ,ДгЖјПЩжЊ
,ДгЖјПЩжЊ![]() .
.
злЩЯЫљЪі: ЫљЧѓ![]() .
.
ЕуОІЃКЕМЪ§ЮЪЬтОГЃЛсгіМћКуГЩСЂЕФЮЪЬтЃК
ЃЈ1ЃЉИљОнВЮБфЗжРыЃЌзЊЛЏЮЊВЛКЌВЮЪ§ЕФКЏЪ§ЕФзюжЕЮЪЬтЃЛ
ЃЈ2ЃЉШє ![]() ОЭПЩЬжТлВЮЪ§ВЛЭЌШЁжЕЯТЕФКЏЪ§ЕФЕЅЕїадКЭМЋжЕвдМАзюжЕЃЌзюжезЊЛЏЮЊ
ОЭПЩЬжТлВЮЪ§ВЛЭЌШЁжЕЯТЕФКЏЪ§ЕФЕЅЕїадКЭМЋжЕвдМАзюжЕЃЌзюжезЊЛЏЮЊ![]() ЃЌШє
ЃЌШє![]() КуГЩСЂ
КуГЩСЂ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() КуГЩСЂЃЌПЩзЊЛЏЮЊ
КуГЩСЂЃЌПЩзЊЛЏЮЊ![]() ЃЈашдкЭЌвЛДІШЁЕУзюжЕЃЉ .
ЃЈашдкЭЌвЛДІШЁЕУзюжЕЃЉ .
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() (
(![]() ЮЊВЮЪ§ЃЉЃЌвд
ЮЊВЮЪ§ЃЉЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсЕФЗЧИКАыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп
жсЕФЗЧИКАыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФМЋзјБъЗНГЬЃЛ
ЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
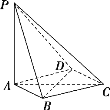
ЁОЬтФПЁПШчЭМЃЌдкЫФРтзЖPABCDжаЃЌPAЁЭЦНУцABCDЃЌЕзУцABCDЪЧСтаЮЃЌABЃН2ЃЌЁЯBADЃН60Ёу.
(1)ЧѓжЄЃКBDЁЭЦНУцPACЃЛ
(2)ШєPAЃН4ЃЌЧѓЦНУцPBCгыЦНУцPDCЫљГЩНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
(1)Шє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
(2)Шє![]() КуГЩСЂЃЌЧѓЪЕЪ§
КуГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНЬхABCDЉA1B1C1D1жаЃЌEЪЧABЕФжаЕуЃЌFдкCC1ЩЯЃЌЧвCFЃН2FC1ЃЌЕуPЪЧВрУцAA1D1DЃЈАќРЈБпНчЃЉЩЯвЛЖЏЕуЃЌЧвPB1ЁЮЦНУцDEFЃЌдђtanЁЯABPЕФШЁжЕЗЖЮЇЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧвЛИівдA1B1C1ЮЊЕзУцЕФжБШ§РтжљБЛвЛЦНУцЫљНиЕУЕНЕФМИКЮЬхЃЌНиУцЮЊABCЃЌвбжЊA1B1ЃНB1C1ЃН2ЃЌЁЯA1B1C1ЃН90ЁуЃЌAA1ЃН4ЃЌBB1ЃН3ЃЌCC1ЃН2ЃЌЧѓЃК

ЃЈ1ЃЉИУМИКЮЬхЕФЬхЛ§ЃЎ
ЃЈ2ЃЉНиУцABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌдк
ЃЌдк![]() ДІЕФЧаЯпЗНГЬЮЊ
ДІЕФЧаЯпЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓ![]() ЃЌ
ЃЌ ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ ![]() ЃЛЃЈ2ЃЉМћНтЮі
ЃЛЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЧѓГіКЏЪ§ЕФЕМЪ§ЃЌЕУЕНЙигк![]() ЕФЗНГЬзщЃЌНтГіМДПЩЃЛ
ЕФЗНГЬзщЃЌНтГіМДПЩЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌСю
ЃЌСю![]() ЃЌ РћгУЕМЪ§баОПЦфЕЅЕїадПЩЕУ
ЃЌ РћгУЕМЪ§баОПЦфЕЅЕїадПЩЕУ
![]() ЃЌ
ЃЌ
ДгЖјжЄУї![]() .
.
ЪдЬтНтЮіЃКЃЈЃЈ1ЃЉгЩЬтвт![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
гж![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌгы
ЃЌгы![]() УЌЖмЃЌЙЪ
УЌЖмЃЌЙЪ![]() ЃЌ
ЃЌ ![]() .
.
ЃЈ2ЃЉгЩЃЈ1ЃЉПЩжЊ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ
Сю![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Сю![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ ![]() ЕЅЕїЕнМѕЃЌЧв
ЕЅЕїЕнМѕЃЌЧв![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЃЌ
ЃЌ ![]() ЕЅЕїЕндіЃЛЧв
ЕЅЕїЕндіЃЛЧв![]() ЃЌ
ЃЌ
Ыљвд![]() дк
дк![]() ЩЯЕБЕЅЕїЕнМѕЃЌдк
ЩЯЕБЕЅЕїЕнМѕЃЌдк![]() ЩЯЕЅЕїЕндіЃЌЧв
ЩЯЕЅЕїЕндіЃЌЧв![]() ЃЌ
ЃЌ
ЙЪ![]() ЃЌ
ЃЌ
ЙЪ![]() .
.
ЁОЕуОІЁПБОЬтПМВщРћгУКЏЪ§ЕФЧаЯпЧѓВЮЪ§ЕФЗНЗЈЃЌвдМАРћгУЕМЪ§жЄУїВЛЕШЪНЕФЗНЗЈЃЌНтЬтЪБвЊШЯецЩѓЬтЃЌзЂвтЕМЪ§аджЪЕФКЯРэдЫгУ.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
22
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЃЌ
ЃЌ ![]() ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЌШєжБЯп
ЃЌШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() ЯрЧаЃЛ
ЯрЧаЃЛ
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФМЋзјБъЗНГЬЃЛ
ЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉдкЧњЯп![]() ЩЯШЁСНЕу
ЩЯШЁСНЕу![]() ЃЌ
ЃЌ ![]() гыдЕу
гыдЕу![]() ЙЙГЩ
ЙЙГЩ![]() ЃЌЧвТњзу
ЃЌЧвТњзу![]() ЃЌЧѓУцЛ§
ЃЌЧѓУцЛ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЁЃ
ЁЃ
ЃЈ1ЃЉШєfЃЈxЃЉЕФЭМЯѓгыgЃЈxЃЉЕФЭМЯѓЫљдкСНЬѕЧњЯпЕФвЛИіЙЋЙВЕудкyжсЩЯЃЌЧвдкИУЕуДІСНЬѕЧњЯпЕФЧаЯпЛЅЯрДЙжБЃЌЧѓbКЭcЕФжЕЁЃ
ЃЈ2ЃЉШєaЃНcЃН1ЃЌbЃН0ЃЌЪдБШНЯfЃЈxЃЉгыgЃЈxЃЉЕФДѓаЁЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєbЃНcЃН0ЃЌжЄУїЃКЖдШЮвтИјЖЈЕФе§Ъ§aЃЌзмДцдке§Ъ§mЃЌЪЙЕУЕБx![]() ЪБЃЌ
ЪБЃЌ
КугаfЃЈxЃЉЃОgЃЈxЃЉГЩСЂЁЃ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com