练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知x,y的取值如下表所示：
    x
    		2
    		3
    		4
    		5
    		6
    y
    		2.2
    		3.8
    		5.5
    		6.5
    		7. 0
    从散点图可以看出x与y线性相关.
    （1）求出线性回归方程.
    （2）请估计x=10时y的值.
    参考数据与公式：
                   
    （1）=1.23x+0.08          （2）=12.38.   
    (1)由公式,,求出回归直线方程.
    (2)把x=10代入（1）中所求回归直线方程可求出y值
    （1）   …………2分
    于是     ……………………4分
    =5-1.23×4=0.08  回归直线方程为=1.23x+0.08  ……8分
    （2）当x=10时，=1.23×10+0.08=12.3+0.08=12.38.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：填空题

    已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是________________.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    对四组不同数据进行统计，分别获得以下散点图，如果对它们的相关系数进行比较，下列结论中正确的是 (      )
         
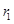    相关系数为                   相关系数为
         
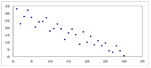
    相关系数为                    相关系数为
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知一组观测值()（）具有线性相关关系,若求得回归直线的斜率,及,,则回归直线方程为
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列关系中，具有相关关系的是（   ）
    A．人的身高与体重；B．匀速行驶的车辆所行驶距离与行驶的时间；
    C．人的身高与视力；D．正方体的体积与边长.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

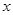    某产品的广告费用与销售额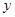的统计数据如下表：
    广告费用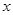（万元）
    		4
    		2
    		3
    		5
    销售额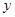（万元）
    		49
    		26
    		39
    		54
    根据上表数据预计广告费用为6万元时,销售额为（      ）
    A．63.6万元      B．65.5万元      C．67.7万元     D．72.0万元

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的值落在（29.94，30.06）的零件为优质品。从两个分厂生产的零件中各抽出500件，量其内径尺寸，的结果如下表：
    甲厂：

    （1）  试分别估计两个分厂生产的零件的优质品率；
    （2）  由于以上统计数据填下面列联表，并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
     
    		甲 厂
    		   乙 厂
    		 合计
    优质品
    		 
    		 
    		 
     非优质品
    		 
    		 
    		 
      合计
    		 
    		 
    		 
    附：，  .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    在下列各图中，相关关系最强的是（ 　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

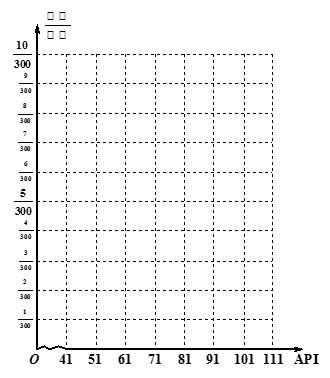
    城市的空气质量以其空气质量指数API（为整数）衡量，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显．根据空气质量指数API的不同，可将空气质量分级如下表：
    API
    		0~50
    		51~100
    		101~150
    		151~200
    		201~250
    		251~300
    		>300
    状况
    		优
    		良
    		轻微污染
    		轻度污染
    		中度污染
    		中度重污染
    		重度污染
     
    为了了解某城市2011年的空气质量情况，现从该城市一年空气质量指数API的监测数据库中，用简单随机抽样方法抽取30个空气质量指数API进行分析，得到如下数据：
    API分组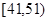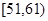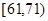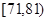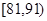







    频数
    		  2
    		    1
    		   4
    		   6
    		  10
    		5
    		  2
     

    （Ⅰ）完成下面频率分布直方图，并求质量指数API的中位数大小；
    （Ⅱ）估计该城市一年中空气质量为优良的概率；
    （Ⅲ）请你依据所给数据和上述分级标准，对该城市的空气质量给出一个简短评价.

    查看答案和解析>>

    同步练习册答案