
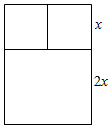
 一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求:
一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求:分析 ①求出窗框的高为3x,宽为$\frac{42-7x}{3}$,推出窗框的面积,求出定义域;
②利用二次函数的最值求法,配方,可得最大值时上、下框架的高;
③由②即可得到最大值.
解答  解:①如图设上框高为x,则竖木料总长=3x+4x=7x
解:①如图设上框高为x,则竖木料总长=3x+4x=7x
三根横木料总长=42-7x,
可得窗框的高为3x,宽为$\frac{42-7x}{3}$,
即窗框的面积为S=3x•$\frac{42-7x}{3}$=-7x2+42x(0<x<6);
②由S=-7x2+42x(0<x<6),
配方得,S=-7(x-3)2+63(0<x<6)
即有当x=3米时,即上框架高为3米、下框架为6米,
光线通过的窗框面积最大;
③光线通过窗框面积最大为63平方米.
点评 本题考查二次函数在实际问题中的运用,考查函数最值的求法,考查分析问题解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}+1$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{12}{5}$] | B. | [0,2] | C. | [2,$\frac{12}{5}$] | D. | [2,$\frac{8}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年重庆市高二上学期入学考试数学试卷(解析版) 题型:解答题
为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
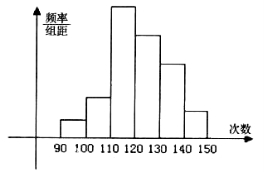
(Ⅰ)求第二小组的频率及样本容量
(Ⅱ)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com