
分析 (1)对条件式两边平方即可解出;
(2)根据向量的数量积得出AB•AC,联立方程组解出AB,AC,BC=|$\overrightarrow{AB}-\overrightarrow{AC}$|=2.
解答 解:(1)∵$\overrightarrow{AB}$$•\overrightarrow{AC}$=|$\overrightarrow{AB}$$-\overrightarrow{AC}$|=2,
∴|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2-2$\overrightarrow{AB}•\overrightarrow{AC}$=4,即|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2-4=4,
∴|$\overrightarrow{AB}$|2+|$\overrightarrow{AC}$|2=8.
(2)∵$\overrightarrow{AB}•\overrightarrow{AC}$=AB•AC•cosA=$\frac{1}{2}$AB•AC=2.
∴AB•AC=4.
∴(AB-AC)2=AB2+AC2-2AB•AC=0.
∴AB=AC=2.
BC=|$\overrightarrow{AB}-\overrightarrow{AC}$|=2.
点评 本题考查了平面向量的数量积运算,向量的三角形法则,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
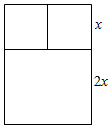 一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求:
一根木料长为42米,要做一个如图的窗框,已知上框架与下框架的高的比为1:2,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届广西南宁二中等校高三8月联考数学(理)试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知直线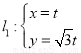 (
( 为参数),圆
为参数),圆 ,以坐标原点为极点,
,以坐标原点为极点,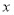 轴的正半轴为极轴建立直角坐标系.
轴的正半轴为极轴建立直角坐标系.
(1)求圆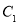 的极坐标方程,直线
的极坐标方程,直线 的极坐标方程;
的极坐标方程;
(2)设 与
与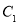 的交点为
的交点为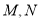 ,求
,求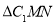 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:选择题
如下图,直三棱柱ABC﹣A1B1C1中,∠ACB=90°,AB=2,BC=1,D为AB中点,则异面直线CD与A1C1所成的角的大小为( )
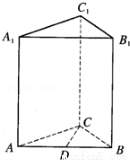
A.90° B.60° C.45° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com