
集合A={x|x2-ax+a2-19=0},B={x|x2-5x+6=0},
C={x|x2+2x-8=0}.
(Ⅰ)若A= ,求a的值;
,求a的值;
(Ⅱ)若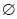
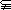 A∩B,A∩C=
A∩B,A∩C=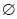 ,求a的值.
,求a的值.
(Ⅰ)5;(Ⅱ)-2
【解析】
试题分析:A∩C=A说明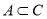 ,A∩B=
,A∩B=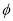 ,所以
,所以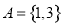 ,再利用韦达定理即可算出p,q的值.另外在解决有关A∩B=A,A∪B=B,
,再利用韦达定理即可算出p,q的值.另外在解决有关A∩B=A,A∪B=B,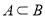 等类型的集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解;另外要注意分类讨论和数形结合思想的应用.
等类型的集合问题时,往往忽略空集的情况,一定先考虑∅是否成立,以防漏解;另外要注意分类讨论和数形结合思想的应用.
试题解析:由已知,得B={2,3},C={2,-4}
(Ⅰ)∵A=B于是2,3是一元二次方程x2-ax+a2-19=0的两个根,
由韦达定理知:
 解之得a=5.
解之得a=5.
(Ⅱ)由A∩B 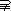
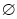
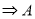 ∩
∩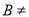
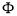 ,又A∩C=
,又A∩C=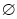 ,
,
得3∈A,2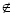 A,-4
A,-4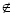 A,
A,
由3∈A,
得32-3a+a2-19=0,解得a=5或a=-2
当a=5时,A={x|x2-5x+6=0}={2,3},与2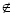 A矛盾;
A矛盾;
当a=-2时,A={x|x2+2x-15=0}={3,-5},符合题意.
∴a=-2.
考点:集合运算


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:2014-2015学年湖北长阳县第一高中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
如图所示,程序框图(算法流程图)的输出结果是( )

A.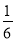 B.
B.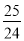 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省高一上学期期中考试数学试卷(解析版) 题型:选择题
设函数 的图象的交点为
的图象的交点为 ,则
,则 所在的区间是( )
所在的区间是( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年北京市高二上学期期中考试数学试卷(解析版) 题型:选择题
如图,定点 ,
, 都在平面
都在平面 内,定点
内,定点 ,
, ,
, 是
是 内异于
内异于 和
和 的动点,且
的动点,且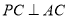 .那么,动点C在平面
.那么,动点C在平面 内的轨迹是( )
内的轨迹是( )

A.一条线段,但要去掉两个点
B.一个圆,但要去掉两个点
C.一个椭圆,但要去掉两个点
D.半圆,但要去掉两个点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com