
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 ,
, ,则有
,则有 .
.
(1)判断 的单调性,并加以证明;
的单调性,并加以证明;
(2)解不等式 ;
;
(3)若 对所有
对所有 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1)增函数,证明过程见解析,(2)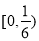 ,(3)
,(3)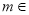
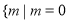 或
或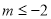 或
或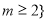 。
。
【解析】
试题分析:(1)根据单调函数的定义,先取值:任取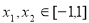 ,且
,且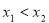 ,然后根据已知条件结合赋值法得
,然后根据已知条件结合赋值法得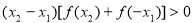 ,再根据奇函数的定义得
,再根据奇函数的定义得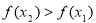 ,
,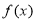 在
在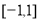 上单增。(2)根据(1)中的单调性,去掉
上单增。(2)根据(1)中的单调性,去掉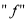 ,要注意函数的定义域,可得
,要注意函数的定义域,可得 ,解该不等式求得
,解该不等式求得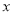 的范围。(3)这是一个不等式恒成立问题,结合(1)可知该不等式可转化为
的范围。(3)这是一个不等式恒成立问题,结合(1)可知该不等式可转化为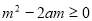 对任意
对任意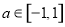 恒成立,然后构造函数
恒成立,然后构造函数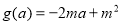 ,
,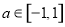 ,这是关于
,这是关于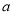 的一次函数,只需保证
的一次函数,只需保证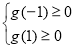 即可。
即可。
试题解析:(1)证:任取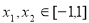 ,且
,且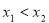 ,则
,则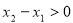 由题意
由题意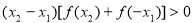
因为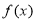 为奇函数,所以
为奇函数,所以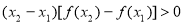
所以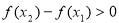 ,即
,即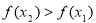 ,所以
,所以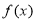 在
在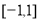 上单增 4分
上单增 4分
(2)由题意得 , 所以
, 所以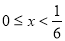 ,故该不等式的解集为
,故该不等式的解集为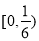 8分
8分
(3)由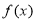 在
在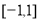 上单增,
上单增,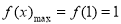 ,由题意,
,由题意,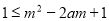 ,
,
即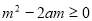 对任意
对任意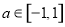 恒成立,令
恒成立,令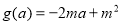 ,
,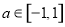
 , 所以
, 所以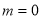 或
或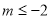 或
或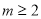
综上所述,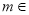
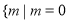 或
或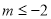 或
或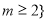 12分
12分
考点:(1)单调函数的定义、奇函数的定义,(2)利用函数的单调性求范围,(3)构造函数解决一元二次不等式恒成立问题。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:解答题
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组得到的频率分布表如下图所示,
班号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| ① | 0.350 |
第3组 |
| 30 | ② |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.00 | |

(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求:第4组至少有一名学生被考官A面试的概率?
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:选择题
在各项都为正数的等比数列{an}中,首项a1=3,前三项和为21,则a3+a4+a 5=( )
A.33 B.72 C.84 D.189
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二上学期10月模块考试数学试卷(解析版) 题型:选择题
设数列 为等差数列,其前n项和为
为等差数列,其前n项和为 ,已知
,已知 ,
,
 ,若对任意
,若对任意 ,都有
,都有 成立,则k的值为( )
成立,则k的值为( )
A.22 B.21 C.20 D.19
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com