练习册系列答案
相关习题
科目:高中数学
来源:四川省南山中学2011-2012学年高二五月月考数学文科试题
题型:013
已知抛物线的焦点坐标是(0,-3),则该抛物线的标准方程为
[ ]
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
函数 的单调减区间为________; 的单调减区间为________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
设数列{an}的前n项和为Sn,令Tn= ,称Tn为数列a1,a2,……,an的“理想数”,已知数列a1,a2,……,a502的“理想数”为2012,那么数列5,a1,a2,……,a502的“理想数”为 ,称Tn为数列a1,a2,……,an的“理想数”,已知数列a1,a2,……,a502的“理想数”为2012,那么数列5,a1,a2,……,a502的“理想数”为
|
| [ ] |
A. |
2008
|
B. |
2014
|
C. |
2012
|
D. |
2013
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知函数f(x)=ln(x-1)+ (a∈R). (a∈R).
(1)若a=2时,试证明:当x≥2时,f(x)≥1;
(2)如果函数y=f(x)是定义域上的增函数,求a的取值范围;
(3)求证:ln(n+1)> + +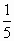 + + +…+ +…+ (n∈N*). (n∈N*).
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 平面解析几何
题型:
|
|
|
设直线l1的参数方程为 (t为参数),直线l2的方程为y=3x+4,则l1与l2间的距离为________. (t为参数),直线l2的方程为y=3x+4,则l1与l2间的距离为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
函数f(x)的导函数为 (x),对任意的x∈R都有2 (x),对任意的x∈R都有2 (x)>f(x)成立,则 (x)>f(x)成立,则
|
| [ ] |
A. |
3f(2ln2)>2f(2ln3)
|
B. |
3f(2ln2)<2f(2ln3)
|
C. |
3f(2ln2)=2f(2ln3)
|
D. |
3f(2ln2)与2f(2ln3)的大小不确定
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
函数 在x等于________处取得极值. 在x等于________处取得极值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教版(大纲版) 高中数学
题型:
|
|
|
已知命题p: x∈R,x2-a≥0,命题q: x∈R,x2-a≥0,命题q: x∈R,x2+2ax+2-a=0,命题“p或q”为假,求实数a的取值范围. x∈R,x2+2ax+2-a=0,命题“p或q”为假,求实数a的取值范围.
|
|
|
查看答案和解析>>
