
分析 由题意,可用插空法求解,把不中的四枪看作是四个格板,格开了五个空隙,再将命中的四枪看作四个物体,由于其中有连中的三枪,此三枪绑定看作是一个物体,先插入此物体,再插入剩余的1个物体,由此计算出所有不同的情况即可选出正确答案.
解答 解:本题可用插空法解决,把不中的四枪看作是四个格板,它们排成一列,分出五个空隙,再将命中的四枪看作是插入五个空隙中的四个物体,由于其中有三枪连中,将它们绑定看作一个物体,然后分两步插入五个空隙:
第一步插入绑定三个物体,有5种方法;
第二步将剩下1个物体插入剩下的四个空隙中,有4种方法,
故总的插入方法有5×4=20(种).
故答案为:20.
点评 本题考点是排列、组合及简单计数问题,考查插空法与绑定法,解答的关键是理解题意将问题正确转化,插空与绑定是计数中常采用的技巧,注意体会其使用的条件.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 合计 | |
| 甲 | 20 | 5 | 25 |
| 乙 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
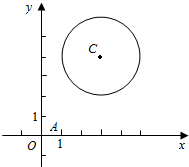 已知圆C:ABCD,直线l1过定点A (1,0).
已知圆C:ABCD,直线l1过定点A (1,0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com