练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆： 的离心率，且过点．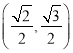

    （1）求椭圆的方程；

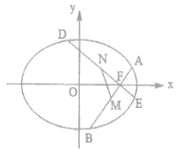
    （2）如图，过椭圆的右焦点作两条相互垂直的直线交椭圆分别于，且满足， ，求面积的最大值．

    【答案】（1）；（2）时， 的面积取得最大值.

    【解析】试题分析：

    (1)利用题意列出 的方程组，求得 的值即可求得椭圆的方程；

    (2)设出直线 的方程，联立直线与椭圆的方程，结合韦达定理求得 的值，则 ，最后利用均值不等式求解三角形面积的最大值即可.

    试题解析：

    （1）根据条件有，解得，所以椭圆．

    （2）根据， 可知， 分别为的中点，且直线斜率均存在且不为0，现设点，直线的方程为，不妨设，联立椭圆有，根据韦达定理得： ， ，

    ， ，同理可得，

    所以面积，现令，

    那么，所以当， 时， 的面积取得最大值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知圆：，直线过定点.

    （1）若与圆相切，求的方程；

    （2）若与圆相交于，两点，求三角形面积的最大值，并求此时的直线方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】即将于年夏季毕业的某大学生准备到贵州非私营单位求职，为了了解工资待遇情况，他在贵州省统计局的官网上，查询到年到年非私营单位在岗职工的年平均工资近似值（单位：万元），如下表：

    年份

    序号

    年平均工资

    （1）请根据上表的数据，利用线性回归模型拟合思想，求关于的线性回归方程（，的计算结果根据四舍五入精确到小数点后第二位）；

    （2）如果毕业生对年平均工资的期望值为8.5万元，请利用（1）的结论，预测年的非私营单位在岗职工的年平均工资（单位：万元。计算结果根据四舍五入精确到小数点后第二位），并判断年平均工资能否达到他的期望.

    参考数据：，，

    附：对于一组具有线性相关的数据：，，，，

    其回归直线的斜率和截距的最小二乘法估计分别为

    ，

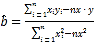
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆与轴交于、两点（点在点的左侧），、是分别过、点的圆的切线，过此圆上的另一个点（点是圆上任一不与、重合的动点）作此圆的切线，分别交、于、两点，且、两直线交于点．

    （）设切点坐标为，求证：切线的方程为．

    （）设点坐标为，试写出与的关系表达式（写出详细推理与计算过程）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

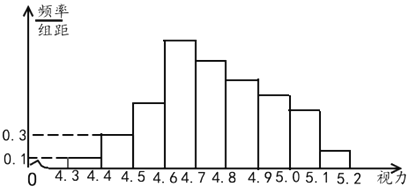
    【题目】如图是由容量为100的样本得到的频率分布直方图．其中前4组的频率成等比数列，后6组的频数成等差数列，设最大频率为a，在到之间的数据个数为b，则a，b的值分别为（ ）

    A.，78

    B.，83

    C.，78

    D.，83

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数其中，为常数且在处取得极值．

    1当时，求的单调区间；

    2若在上的最大值为1，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某单位全体员工年龄频率分布表为：

    年龄（岁）

    [25，30）

    [30，35）

    [35，40）

    [40，45）

    [45，50）

    [50，55）

    合计

    人数（人）

    6

    18

    50

    31

    19

    16

    140

    经统计，该单位35岁以下的青年职工中，男职工和女职工人数相等，且男职工的年龄频率分布直方图和如图所示：

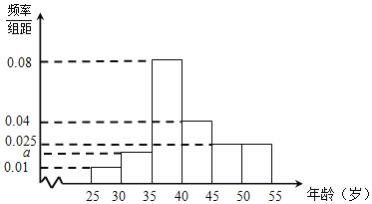
    （Ⅰ）求a；

    （Ⅱ）求该单位男女职工的比例；

    （Ⅲ）若从年龄在[25，30）岁的职工中随机抽取两人参加某项活动，求恰好抽取一名男职工和一名女职工的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,棱长为的正方体的顶点在平面内,三条棱,,都在平面的同侧. 若顶点,到平面的距离分别为,;

    （1）求平面与平面所成锐二面角的余弦值;

    （2）求顶点到面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线的离心率为2，左右焦点分别为，，过右焦点且垂直于x轴的直线与双曲线交于A，B两点，且的周长为．

    （1）求双曲线C的方程；

    （2）已知直线，点P是双曲线C上的动点，求点P到直线l的距离的最小值．

    查看答案和解析>>

    同步练习册答案