
【题目】圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 、
、![]() 是分别过
是分别过![]() 、
、![]() 点的圆
点的圆![]() 的切线,过此圆上的另一个点
的切线,过此圆上的另一个点![]() (
(![]() 点是圆上任一不与
点是圆上任一不与![]() 、
、![]() 重合的动点)作此圆的切线,分别交
重合的动点)作此圆的切线,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两直线交于点
两直线交于点![]() .
.
(![]() )设切点
)设切点![]() 坐标为
坐标为![]() ,求证:切线
,求证:切线![]() 的方程为
的方程为![]() .
.
(![]() )设点
)设点![]() 坐标为
坐标为![]() ,试写出
,试写出![]() 与
与![]() 的关系表达式(写出详细推理与计算过程).
的关系表达式(写出详细推理与计算过程).
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
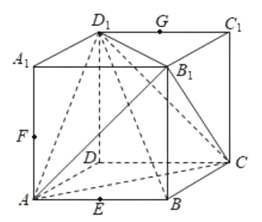
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
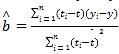 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,A是椭圆短轴的一个端点,直线AF与椭圆另一交点为B,且
,A是椭圆短轴的一个端点,直线AF与椭圆另一交点为B,且![]() .
.
(1)求椭圆方程;
(2)若斜率为1的直线l交椭圆于C,D,且CD为底边的等腰三角形的顶点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点且满足
上一点且满足![]() ,
,![]() 是线段
是线段![]() 上一动点,把
上一动点,把![]() 沿
沿![]() 折起得到
折起得到![]() ,使得平面
,使得平面![]() 平面
平面![]() ,分别记
,分别记![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成锐角为
所成锐角为![]() ,则:( )
,则:( )

![]()
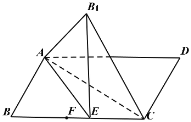
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校在2018年的自主招生考试成绩中随机抽取100名学生的笔试成绩,折合成标准分后,最高分是10分.按成绩共分成五组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10),得到的频率分布直方图如图所示:
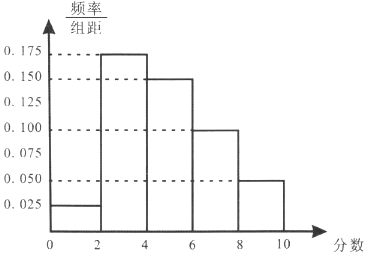
(1)分别求第三,四,五组的频率;
(2)该学校在第三,四,五组中用分层抽样的方法抽取6名同学.
①已知甲同学和乙同学均在第三组,求甲、乙同时被选中的概率
②若在这6名同学中随机抽取2名,设第4组中有X名同学,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com