
【题目】已知圆![]() ,
,![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆外,过点
在圆外,过点![]() 作圆
作圆![]() 的切线,设切点为
的切线,设切点为![]() .
.
(1)若点![]() 运动到
运动到![]() 处,求此时切线
处,求此时切线![]() 的方程;
的方程;
(2)求满足![]() 的点
的点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() 或
或![]() ; (2)
; (2)![]() .
.
【解析】
试题分析:(1)当过点P的切线斜率存在时,由点斜式设出切线方程,再利用圆心到切线的距离等于半径求得k的值,可得切线方程.当切线斜率不存在时,要检验是否满足条件,从而得出结论. (2)设点![]() ,由圆的切线的性质知,
,由圆的切线的性质知,![]() 为直角三角形,可得
为直角三角形,可得![]() ,
,![]() ;由
;由![]() ,化简可得点P的轨迹方程为
,化简可得点P的轨迹方程为![]() .
.
试题解析:
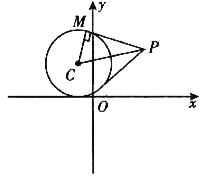
解: 把圆C的方程化为标准方程为(x+1)2+(y-2)2=4,
∴圆心为C(-1,2),半径r=2.
(1)当l的斜率不存在时,此时l的方程为x=1,C到l的距离d=2=r,满足条件.
当l的斜率存在时,设斜率为k,得l的方程为y-3=k(x-1),即kx-y+3-k=0,
则![]() =2,解得k=
=2,解得k=![]() .
.
∴l的方程为y-3=![]() (x-1),
(x-1),
即3x+4y-15=0.
综上,满足条件的切线l的方程为![]() 或
或![]() .
.
(2)设P(x,y),则|PM|2=|PC|2-|MC|2=(x+1)2+(y-2)2-4,
|PO|2=x2+y2,
∵|PM|=|PO|.
∴(x+1)2+(y-2)2-4=x2+y2,
整理,得2x-4y+1=0,
∴点P的轨迹方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(cosθ,sinθ),
=(cosθ,sinθ), ![]() =(﹣
=(﹣ ![]() ,
, ![]() );
);
(1)若 ![]() ∥
∥ ![]() ,且θ∈(0,π),求θ;
,且θ∈(0,π),求θ;
(2)若|3 ![]() +
+ ![]() |=|
|=| ![]() ﹣3
﹣3 ![]() |,求|
|,求| ![]() +
+ ![]() |的值.
|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若两直线![]() 的倾斜角分别为
的倾斜角分别为![]() 与
与![]() ,则下列四个命题中正确的是( )
,则下列四个命题中正确的是( )
A. 若![]() <
<![]() ,则两直线的斜率:k1 < k2 B. 若
,则两直线的斜率:k1 < k2 B. 若![]() =
=![]() ,则两直线的斜率:k1= k2
,则两直线的斜率:k1= k2
C. 若两直线的斜率:k1 < k2 ,则![]() <
<![]() D. 若两直线的斜率:k1= k2 ,则
D. 若两直线的斜率:k1= k2 ,则![]() =
=![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在x=x0处取得极大值或极小值,则称x0为函数y=f(x)的极值点.已知a,b是实数,1和-1是函数f(x)=x3+ax2+bx的两个极值点.
(1)求a和b的值;
(2)设函数g(x)的导函数g′(x)=f(x)+2,求g(x)的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆![]() 离心率是
离心率是![]() ,焦点到相应准线的距离是3.
,焦点到相应准线的距离是3.
(1)求椭圆的方程;
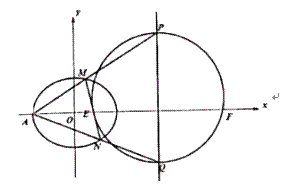
(2)如图,设A是椭圆的左顶点,动圆过定点E(1,0)和F(7,0),且与直线x=4交于点P,Q.
①求证:AP,AQ斜率的积是定值;
②设AP,AQ分别与椭圆交于点M,N,求证:直线MN过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东60°,向北航行40分钟后到达B点,测得油井P在南偏东30°,海轮改为北偏东60°的航向再行驶80分钟到达C点,求P、C间的距离( )海里. 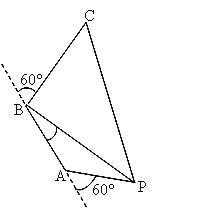
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com