
【题目】在平面直角坐标系xOy中,已知椭圆![]() 离心率是
离心率是![]() ,焦点到相应准线的距离是3.
,焦点到相应准线的距离是3.
(1)求椭圆的方程;
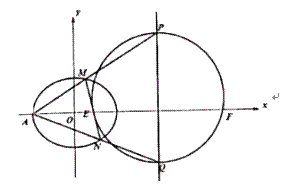
(2)如图,设A是椭圆的左顶点,动圆过定点E(1,0)和F(7,0),且与直线x=4交于点P,Q.
①求证:AP,AQ斜率的积是定值;
②设AP,AQ分别与椭圆交于点M,N,求证:直线MN过定点.
【答案】(1)![]() ;(2)①见解析;②见解析.
;(2)①见解析;②见解析.
【解析】
(1)由椭圆的离心率得到![]() ,结合焦点到相应准线的距离可求出
,结合焦点到相应准线的距离可求出![]() 的值,进而求出
的值,进而求出![]() 的值,即可得出椭圆的方程;(2) ①设动圆圆心坐标为
的值,即可得出椭圆的方程;(2) ①设动圆圆心坐标为![]() ,进而写出动圆的方程,将直线
,进而写出动圆的方程,将直线![]() 的方程代入圆的方程,得出点
的方程代入圆的方程,得出点![]() 两点的纵坐标之积,再利用斜率公式可得出
两点的纵坐标之积,再利用斜率公式可得出![]() 的斜率之积为定值;②设直线
的斜率之积为定值;②设直线![]() 的方程为
的方程为![]() ,将直线
,将直线![]() 的方程与椭圆的方程联立,可得
的方程与椭圆的方程联立,可得![]() ,由
,由![]() 两点的纵坐标之积为
两点的纵坐标之积为![]() ,结合韦达定理计算出
,结合韦达定理计算出![]() ,从而得出直线
,从而得出直线![]() 过定点
过定点![]() .
.
(1)设椭圆的焦距为![]() ,由题意可得
,由题意可得![]() ,所以,
,所以,![]() ,
,
因为椭圆的焦点到相应准线的距离为![]() ,得c=1,所以,
,得c=1,所以,![]() ,
,
因此,椭圆的方程为![]() ;
;
(2)①设动圆的圆心坐标为![]() ,则圆的方程为
,则圆的方程为![]() ,
,
设点![]() ,令
,令![]() ,可得
,可得![]() ,
,
则AP、AQ的斜率之积为![]() (定值);
(定值);
②设直线MN的方程为![]() ,设点
,设点![]()
将直线MN的方程代入椭圆方程并化简得![]() ,
,
由韦达定理可得![]()
因为A、M、P三点共线,则![]() ,
,
由于![]() ,
,![]() ,
,
所以![]() ,则
,则![]() ,同理可得
,同理可得![]()
由![]()
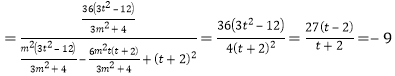 ,解得t=1,
,解得t=1,
因此,直线MN过定点(1,0).


科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线y=﹣2x+1与圆O:x2+y2=r2(r>0)交于M,N两点,且MN=![]() .
.
(1)求M,N的坐标;
(2)求过O,M,N三点的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果数列a1 , a2 , a3 , … , an , …是等差数列,那么下列数列中不是等差数列的是:( )
A.a1+x , a2+x , a3+x , …,an+x ,
B.ka1 , ka2 , ka3 , …,kan ,
C.![]()
D.a1 , a4 , a7 , …a3n﹣2 ,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四个结论: ①数列可以看作是一个定义在正整数集(或它的有限子集{1,2,3……,n})上的函数;
②数列若用图象表示,从图象上看都是一群孤立的点;
③数列的项数是无限的;
④数列通项的表示式是唯一的.
其中正确的是( )
A.①②
B.①②③
C.②③
D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥底面ABC,![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
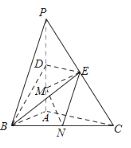
(1)求证:MN∥平面BDE;
(2)求二面角C-EM-N的正弦值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=AP=4,AB=BC=2,M为PC的中点. 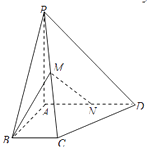
(1)求异面直线AP,BM所成角的余弦值;
(2)点N在线段AD上,且AN=λ,若直线MN与平面PBC所成角的正弦值为 ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com