
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点且满足
上一点且满足![]() ,
,![]() 是线段
是线段![]() 上一动点,把
上一动点,把![]() 沿
沿![]() 折起得到
折起得到![]() ,使得平面
,使得平面![]() 平面
平面![]() ,分别记
,分别记![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成锐角为
所成锐角为![]() ,则:( )
,则:( )

![]()
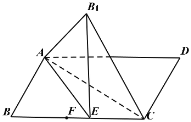
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】在中国国际大数据产业博览会期间,有甲、乙、丙、丁4名游客准备到贵州的黄果树瀑布、梵净山、万峰林三个景点旅游参观,其中的每个人只去一个景点,每个景点至少要去一个人,则游客甲去梵净山的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 、
、![]() 是分别过
是分别过![]() 、
、![]() 点的圆
点的圆![]() 的切线,过此圆上的另一个点
的切线,过此圆上的另一个点![]() (
(![]() 点是圆上任一不与
点是圆上任一不与![]() 、
、![]() 重合的动点)作此圆的切线,分别交
重合的动点)作此圆的切线,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 两直线交于点
两直线交于点![]() .
.
(![]() )设切点
)设切点![]() 坐标为
坐标为![]() ,求证:切线
,求证:切线![]() 的方程为
的方程为![]() .
.
(![]() )设点
)设点![]() 坐标为
坐标为![]() ,试写出
,试写出![]() 与
与![]() 的关系表达式(写出详细推理与计算过程).
的关系表达式(写出详细推理与计算过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位全体员工年龄频率分布表为:
年龄(岁) | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) | [50,55) | 合计 |
人数(人) | 6 | 18 | 50 | 31 | 19 | 16 | 140 |
经统计,该单位35岁以下的青年职工中,男职工和女职工人数相等,且男职工的年龄频率分布直方图和如图所示:
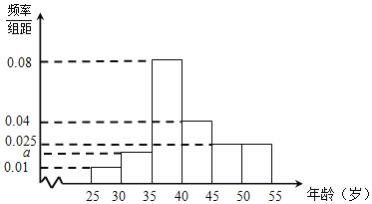
(Ⅰ)求a;
(Ⅱ)求该单位男女职工的比例;
(Ⅲ)若从年龄在[25,30)岁的职工中随机抽取两人参加某项活动,求恰好抽取一名男职工和一名女职工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,棱长为![]() 的正方体的顶点
的正方体的顶点![]() 在平面
在平面![]() 内,三条棱
内,三条棱![]() ,
,![]() ,
,![]() 都在平面
都在平面![]() 的同侧. 若顶点
的同侧. 若顶点![]() ,
,![]() 到平面
到平面![]() 的距离分别为
的距离分别为![]() ,
,![]() ;
;

(1)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(2)求顶点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某职业学校有2000名学生,校服务部为了解学生在校的月消费情况,随机调查了100名学生,并将统计结果绘成直方图如图所示.
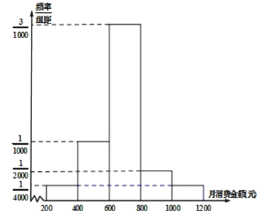
(1)试估计该校学生在校月消费的平均数;
(2)根据校服务部以往的经验,每个学生在校的月消费金额![]() (元)和服务部可获得利润
(元)和服务部可获得利润![]() (元),满足关系式:
(元),满足关系式: 根据以上抽样调查数据,将频率视为概率,回答下列问题:
根据以上抽样调查数据,将频率视为概率,回答下列问题:
(i)将校服务部从一个学生的月消费中,可获得的利润记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
(ii)若校服务部计划每月预留月利润的![]() ,用于资助在校月消费低于400元的学生,估计受资助的学生每人每月可获得多少元?
,用于资助在校月消费低于400元的学生,估计受资助的学生每人每月可获得多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 分别是圆心在原点,半径为
分别是圆心在原点,半径为![]() 和
和![]() 的圆上的动点.动点
的圆上的动点.动点![]() 从初始位置
从初始位置![]() 开始,按逆时针方向以角速度
开始,按逆时针方向以角速度![]() 作圆周运动,同时点
作圆周运动,同时点![]() 从初始位置
从初始位置![]() 开始,按顺时针方向以角速度
开始,按顺时针方向以角速度![]() 作圆周运动.记
作圆周运动.记![]() 时刻,点
时刻,点![]() 的纵坐标分别为
的纵坐标分别为![]() .
.
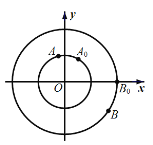
(Ⅰ)求![]() 时刻,
时刻,![]() 两点间的距离;
两点间的距离;
(Ⅱ)求![]() 关于时间
关于时间![]() 的函数关系式,并求当
的函数关系式,并求当![]() 时,这个函数的值域.
时,这个函数的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com