
【题目】在中国国际大数据产业博览会期间,有甲、乙、丙、丁4名游客准备到贵州的黄果树瀑布、梵净山、万峰林三个景点旅游参观,其中的每个人只去一个景点,每个景点至少要去一个人,则游客甲去梵净山的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先求得所有基本事件的个数,再求甲去梵净山的所有情况:根据题意,分2种情况讨论:①,甲单独一个人去梵净山,②,甲和乙、丙、丁中1人去梵净山,分别求出每一种情况的方案的数目相加,由古典概型概率公式计算可得答案.
根据题意,满足每个人只去一个景点,每个景点至少要去一个人的所有基本事件的个数为C42 A33=36种,
若满足甲去梵净山,需要分2种情况讨论:
①,甲单独一个人去梵净山, 将其他3人分成2组,对应剩下的2个景点,有C31A22=6种情况,则此时有6种方案;
②,甲和乙、丙、丁中1人一起旅游,
先在乙、丙、丁中任选1人,与甲一起去梵净山,有C31=3种情况,
将剩下的2人全排列,对应剩下的2个景点,有A22=2种情况,
则此时有2×3=6种方案;
则甲去梵净山的方案有6+6=12种;
所以甲去梵净山的概率为![]() .
.
故选:B.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:高中数学 来源: 题型:
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:

并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买这款电视机 | 不愿意购买这款电视机 | 总计 | |
40岁以上 | 800 | 1000 | |
40岁以下 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在![]() 和
和![]() 的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在
的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在![]() 内的概率.
内的概率.
附: | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为
的棱长为![]() ,点E,F,G分别为棱AB,
,点E,F,G分别为棱AB,![]() ,
,![]() 的中点,下列结论中,正确结论的序号是___________.
的中点,下列结论中,正确结论的序号是___________.
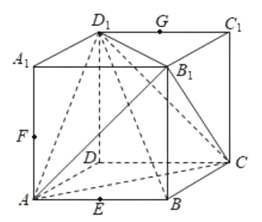
①过E,F,G三点作正方体的截面,所得截面为正六边形;
②![]() 平面EFG;
平面EFG;
③![]() 平面
平面![]() ;
;
④异面直线EF与![]() 所成角的正切值为
所成角的正切值为![]() ;
;
⑤四面体![]() 的体积等于
的体积等于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝国庆节,某中学团委组织了“歌颂祖国,爱我中华”知识竞赛,从参加考试的学生中抽出60名,将其成绩(成绩均为整数)分成[40,50),[50,60),…,[90,100)六组,并画出如图所示的部分频率分布直方图,观察图形,回答下列问题:
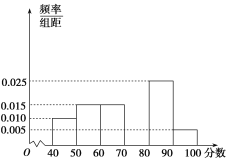
(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次考试的及格率(60分及以上为及格)和平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cos2B+cosB=1-cosAcosC.
(1)求证:a,b,c成等比数列;
(2)若b=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有关于![]() 的一元二次方程
的一元二次方程![]() .
.
(Ⅰ)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数,![]() 是从
是从![]() 三个数中任取的一个数,求上述方程有实根的概率.
三个数中任取的一个数,求上述方程有实根的概率.
(Ⅱ)若![]() 是从区间
是从区间![]() 任取的一个数,
任取的一个数,![]() 是从区间
是从区间![]() 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
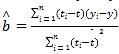 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点且满足
上一点且满足![]() ,
,![]() 是线段
是线段![]() 上一动点,把
上一动点,把![]() 沿
沿![]() 折起得到
折起得到![]() ,使得平面
,使得平面![]() 平面
平面![]() ,分别记
,分别记![]() ,
,![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() ,平面
,平面![]() 与平面
与平面![]() 所成锐角为
所成锐角为![]() ,则:( )
,则:( )

![]()
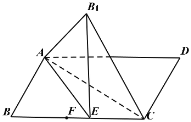
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com