
【题目】已知动直线![]() 垂直于
垂直于![]() 轴,与椭圆
轴,与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上,
上,![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,与曲线
,与曲线![]() 相切于点
相切于点![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】
(1)设出![]() 两点的坐标,根据对称性得到
两点的坐标,根据对称性得到![]() 点坐标,利用平面向量数量积的坐标运算化简
点坐标,利用平面向量数量积的坐标运算化简![]() ,求得
,求得![]() 两点坐标的关系,将
两点坐标的关系,将![]() 点坐标代入椭圆方程,化简求得点
点坐标代入椭圆方程,化简求得点![]() 的轨迹方程.
的轨迹方程.
(2)当直线![]() 斜率不存在时,根据椭圆的几何性质求得
斜率不存在时,根据椭圆的几何性质求得![]() .当直线
.当直线![]() 的斜率存在时,设出直线
的斜率存在时,设出直线![]() 的方程
的方程![]() ,代入
,代入![]() 方程,利用判别式为零列出
方程,利用判别式为零列出![]() 关系.将
关系.将![]() 代入
代入![]() 方程,化简后写出韦达定理,计算出
方程,化简后写出韦达定理,计算出![]() 的表达式,并利用换元法和二次函数的性质,求得
的表达式,并利用换元法和二次函数的性质,求得![]() 的取值范围.
的取值范围.
(1)设![]() ,则由题知
,则由题知![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
由![]() 在椭圆
在椭圆![]() 上,得
上,得![]() ,所以
,所以![]() ,
,
故点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() ;
;
(2)当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 为
为![]() 的左(或右)顶点,也是
的左(或右)顶点,也是![]() 的左(或右)焦点,所以
的左(或右)焦点,所以![]() ;
;
当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,
,
 ,
,![]() ,
,
![]() ,所以
,所以![]() ,
,
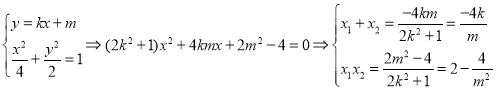 ,
,

令![]() ,
,![]() ,
,![]() ,
,
所以,当![]() 时,即
时,即![]() 时,
时,![]() 取最大值
取最大值![]() ,当
,当![]() 时,即
时,即![]() 时,
时,![]() 取最小值
取最小值![]() ;综上:
;综上:![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】对于任意![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(1)已知数列:1,![]() ,
,![]() 是“K数列”,求实数m的取值范围;
是“K数列”,求实数m的取值范围;
(2)是否存在首项为-1的无穷等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足:
满足:![]() ,若存在,求出
,若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3)已知各项均为正整数的等比数列![]() (至少有4项)为“K数列”,数列
(至少有4项)为“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,是否存在
,是否存在![]() ,使
,使![]() 为“K数列”?若存在,请求出,
为“K数列”?若存在,请求出,![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的图象经过变换
的图象经过变换![]() 后所得的图象对应的函数与
后所得的图象对应的函数与![]() 的值域相同,则称变换
的值域相同,则称变换![]() 是
是![]() 的同值变换,下面给出了四个函数与对应的变换:①
的同值变换,下面给出了四个函数与对应的变换:①![]() ,
, ![]() 将函数
将函数![]() 的图象关于直线
的图象关于直线![]() 作对称变换;②
作对称变换;②![]() ,
, ![]() 将函数
将函数![]() 的图象关于
的图象关于![]() 轴作对称变换;③
轴作对称变换;③![]() ,
, ![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换;④
作对称变换;④![]() ,
,![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换.其中
作对称变换.其中![]() 是
是![]() 的同值变换的有__________(写出所有符合题意的序号)
的同值变换的有__________(写出所有符合题意的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个角形海湾![]() (常数
(常数![]() 为锐角).拟用长度为
为锐角).拟用长度为![]() (
(![]() 为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一:如图1,围成扇形养殖区
为常数)的围网围成一个养殖区,有以下两种方案可供选择:方案一:如图1,围成扇形养殖区![]() ,其中
,其中![]() ;方案二:如图2,围成三角形养殖区
;方案二:如图2,围成三角形养殖区![]() ,其中
,其中![]() .
.
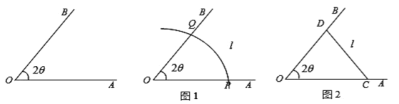
(1)求方案一中养殖区的面积![]() ;
;
(2)求方案二中养殖区的最大面积(用![]() 表示);
表示);
(3)为使养殖区的面积最大,应选择何种方案?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为F1、F2,且过点
的左、右焦点为别为F1、F2,且过点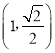 和
和 .
.

(1)求椭圆的标准方程;
(2)如图,点A为椭圆上一位于x轴上方的动点,AF2的延长线与椭圆交于点B,AO的延长线与椭圆交于点C,求△ABC面积的最大值,并写出取到最大值时直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
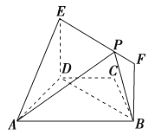
(1)求证:AD⊥平面BFED;
(2)点P在线段EF上运动,设平面PAB与平面ADE所成锐二面角为θ,试求θ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com