
【题目】已知函数f(x)=cos xsin 2x,下列结论中正确的是________(填入正确结论的序号).
①y=f(x)的图象关于点(2π,0)中心对称;
②y=f(x)的图象关于直线x=π对称;
③f(x)的最大值为![]() ;
;
④f(x)既是奇函数,又是周期函数.
【答案】①④
【解析】依题意,对于①,f(4π-x)=cos(4π-x)·sin[2(4π-x)]=-cos x·sin 2x=-f(x),因此函数y=f(x)的图象关于点(2π,0)中心对称,①正确;对于②,f![]() =
=![]() ,f
,f![]() =-
=-![]() ,因此f
,因此f![]() ≠f
≠f![]() ,函数y=f(x)的图象不关于直线x=π对称,②不正确;对于③,f(x)=2sin xcos2x=2(sin x-sin3x);令t=sin x,则y=2(t-t3),t∈[-1,1],y′=2(1-3t2),当-
,函数y=f(x)的图象不关于直线x=π对称,②不正确;对于③,f(x)=2sin xcos2x=2(sin x-sin3x);令t=sin x,则y=2(t-t3),t∈[-1,1],y′=2(1-3t2),当-![]() <t<
<t<![]() 时,y′>0;当-1≤t<-
时,y′>0;当-1≤t<-![]() 或
或![]() <t≤1时,y′<0,因此函数y=2(t-t3)在[-1,1]上的最大值是y=2
<t≤1时,y′<0,因此函数y=2(t-t3)在[-1,1]上的最大值是y=2![]() =
=![]() ,即函数f(x)的最大值是
,即函数f(x)的最大值是![]() ,③不正确;对于④,f(-x)=-f(x),且f(2π+x)=2sin(2π+x)cos2(2π+x)=2sin xcos2x=f(x),因此函数f(x)既是奇函数,又是周期函数,④正确.综上所述,其中正确的结论是①④.
,③不正确;对于④,f(-x)=-f(x),且f(2π+x)=2sin(2π+x)cos2(2π+x)=2sin xcos2x=f(x),因此函数f(x)既是奇函数,又是周期函数,④正确.综上所述,其中正确的结论是①④.


科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,图中(1)、(2)、(3)、(4)为她们刺锈最简单的四个图案,这些图案都是由小正方向构成,小正方形数越多刺锈越漂亮,向按同样的规律刺锈(小正方形的摆放规律相同),设第![]() 个图形包含
个图形包含![]() 个小正方形
个小正方形

(1)求![]() 的值
的值
(2)求出![]() 的表达式
的表达式
(3)求证:当![]() 时,
时, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示![]() .
.
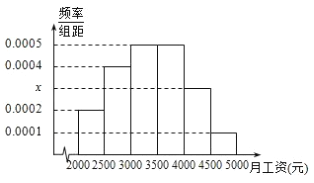
(1)求毕业大学生月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,必须按月收入再从这10000人中按分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽取多少人?
的这段应抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出![]() 盒该产品获利润
盒该产品获利润![]() 元;未售出的产品,每盒亏损
元;未售出的产品,每盒亏损![]() 元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了
元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示,该同学为这个开学季购进了![]() 盒该产品,以
盒该产品,以![]() (单位:盒,
(单位:盒, ![]() )表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
)表示这个开学季内的市场需求量,(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量![]() 的中位数;
的中位数;
(2)将![]() 表示为
表示为![]() 的函数;
的函数;
(3)根据直方图估计利润不少于![]() 元的概率.
元的概率.
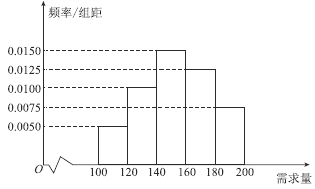
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCDA1B1C1D1中,AB=AA1=1,E为BC中点.
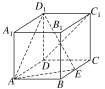
(1)求证:C1D⊥D1E;
(2)在棱AA1上是否存在一点M,使得BM∥平面AD1E?若存在,求![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若二面角B1AED1的大小为90°,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C的中心在原点,其一个焦点与抛物线y2=4![]() x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.
x的焦点相同,又椭圆C上有一点M(2,1),直线l平行于OM且与椭圆C交于A,B两点,连接MA,MB.

(1)求椭圆C的方程;
(2)当MA,MB与x轴所构成的三角形是以x轴上所在线段为底边的等腰三角形时,求直线l在y轴上截距的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com