
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 把sin(x+70°)转化为sin(x+10°+60°)利用两次两角和公式化简,利用正弦函数的性质求得最小值.
解答 解:f(x)=sin(x+10°)+sin(x+70°)
=sin(x+10°)+sin(x+10°+60°)
=sin(x+10°)+$\frac{1}{2}$sin(x+10°)+$\frac{\sqrt{3}}{2}$cos(x+10°)
=$\frac{3}{2}$sin(x+10°)+$\frac{\sqrt{3}}{2}$cos(x+10°)
=$\sqrt{3}$sin(x+10°+30°)
=$\sqrt{3}$sin(x+40°),
∴当sin(x+40°)=1时,函数有最大值.
点评 本题主要考查了两角和公式的运用,三角函数的图象与性质.考查了学生对三角函数公式熟练记忆.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
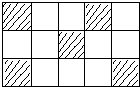
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 22 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com