
| A. | $\frac{5}{4}$ | B. | $\frac{24}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{24}$ |
分析 由已知可得$\overrightarrow{OA}=t\overrightarrow{OP}$,且|$\overrightarrow{OA}$|=|t||$\overrightarrow{OP}$|.有$\left\{\begin{array}{l}{{x}_{P}=\frac{{x}_{A}}{t}}\\{{y}_{P}=\frac{{y}_{A}}{t}}\end{array}\right.$,将点($\frac{{x}_{A}}{t},\frac{{y}_{A}}{t}$)代入双曲线中得${{x}_{A}}^{2}=\frac{16{{y}_{A}}^{2}}{9}+16{t}^{2}$,由|$\overrightarrow{OA}$|•|$\overrightarrow{OP}$|=$\frac{25{{y}_{P}}^{2}}{9|t|}+16|t|$t||$\overrightarrow{OP}$|2=64.得|t|($\frac{{{x}_{A}}^{2}}{{t}^{2}}+\frac{{{y}_{A}}^{2}}{{t}^{2}}$)=6,即得64=$\frac{25{{y}_{P}}^{2}}{9|t|}+16|t|$$≥\frac{40}{3}{y}_{P}$,|yP|$≤\frac{24}{5}$,|$\overrightarrow{OB}•$$\overrightarrow{OP}$|=|yP|$≤\frac{24}{5}$.
解答 解:∵$\overrightarrow{PA}=(t-1)\overrightarrow{OP}$,∴$\overrightarrow{PA}=t\overrightarrow{OP}-\overrightarrow{OP}$,∴$\overrightarrow{OA}=t\overrightarrow{OP}$,且|$\overrightarrow{OA}$|=|t||$\overrightarrow{OP}$|.
∴(xA,yA)=t(xP,yP),∴$\left\{\begin{array}{l}{{x}_{P}=\frac{{x}_{A}}{t}}\\{{y}_{P}=\frac{{y}_{A}}{t}}\end{array}\right.$,将点($\frac{{x}_{A}}{t},\frac{{y}_{A}}{t}$)代入双曲线中得:$\frac{{{x}_{A}}^{2}}{16{t}^{2}}-\frac{{{y}_{A}}^{2}}{9{t}^{2}}=1$.
∴${{x}_{A}}^{2}=\frac{16{{y}_{A}}^{2}}{9}+16{t}^{2}$…①,∵$\overrightarrow{OA}•\overrightarrow{OP}=64$,∴|$\overrightarrow{OA}$|•|$\overrightarrow{OP}$|=$\frac{25{{y}_{P}}^{2}}{9|t|}+16|t|$t||$\overrightarrow{OP}$|2=64.
∴|t|($\frac{{{x}_{A}}^{2}}{{t}^{2}}+\frac{{{y}_{A}}^{2}}{{t}^{2}}$)=64…②
由①②得64=$\frac{25{{y}_{P}}^{2}}{9|t|}+16|t|$$≥\frac{40}{3}{y}_{P}$,∴|yP|$≤\frac{24}{5}$,
|$\overrightarrow{OB}•$$\overrightarrow{OP}$|=|yP|$≤\frac{24}{5}$,
故选:B
点评 本题考查了向量与双曲线,方程思想、转化思想,属于中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}+\frac{4}{5}i$ | B. | $\frac{3}{5}-\frac{4}{5}i$ | C. | $\frac{5}{3}-\frac{5}{4}i$ | D. | $\frac{4}{5}-\frac{3}{5}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{13}$ | B. | 8 | C. | $\frac{{8\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{13}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 5 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
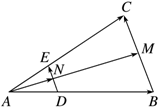 如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )
如图,在△ABC中,$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$,DE∥BC交AC于E,BC边上的中线AM交DE于N,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,用$\overrightarrow a$,$\overrightarrow{b}$表示向量$\overrightarrow{AN}$.则$\overrightarrow{AN}$等于( )| A. | $\frac{1}{2}$($\overrightarrow a$+$\overrightarrow{b}$) | B. | $\frac{1}{3}$( $\overrightarrow a$+$\overrightarrow{b}$) | C. | $\frac{1}{6}$( $\overrightarrow a$+$\overrightarrow{b}$) | D. | $\frac{1}{8}$( $\overrightarrow a$+$\overrightarrow{b}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com