
分析 (1)题干求导可知f′(x)=$\frac{(2ax+1)(x+1)}{x}$(x>0),分a=0、a>0、a<0三种情况讨论f′(x)与0的大小关系可得结论;
(2)通过(1)可知f(x)max=f(-$\frac{1}{2a}$)=-1-ln2-$\frac{1}{4a}$+ln(-$\frac{1}{a}$),进而转化可知问题转化为证明:当t>0时-$\frac{1}{2}$t+lnt≤-1+ln2.进而令g(t)=-$\frac{1}{2}$t+lnt,利用导数求出y=g(t)的最大值即可.
解答 (1)解:因为f(x)=lnx+ax2+(2a+1)x,
求导f′(x)=$\frac{1}{x}$+2ax+(2a+1)=$\frac{2a{x}^{2}+(2a+1)x+1}{x}$=$\frac{(2ax+1)(x+1)}{x}$,(x>0),
①当a=0时,f′(x)=$\frac{1}{x}$+1>0恒成立,此时y=f(x)在(0,+∞)上单调递增;
②当a>0,由于x>0,所以(2ax+1)(x+1)>0恒成立,此时y=f(x)在(0,+∞)上单调递增;
③当a<0时,令f′(x)=0,解得:x=-$\frac{1}{2a}$.
因为当x∈(0,-$\frac{1}{2a}$)f′(x)>0、当x∈(-$\frac{1}{2a}$,+∞)f′(x)<0,
所以y=f(x)在(0,-$\frac{1}{2a}$)上单调递增、在(-$\frac{1}{2a}$,+∞)上单调递减.
综上可知:当a≥0时f(x)在(0,+∞)上单调递增,
当a<0时,f(x)在(0,-$\frac{1}{2a}$)上单调递增、在(-$\frac{1}{2a}$,+∞)上单调递减;
(2)证明:由(1)可知:当a<0时f(x)在(0,-$\frac{1}{2a}$)上单调递增、在(-$\frac{1}{2a}$,+∞)上单调递减,
所以当x=-$\frac{1}{2a}$时函数y=f(x)取最大值f(x)max=f(-$\frac{1}{2a}$)=-1-ln2-$\frac{1}{4a}$+ln(-$\frac{1}{a}$).
从而要证f(x)≤-$\frac{3}{4a}$-2,即证f(-$\frac{1}{2a}$)≤-$\frac{3}{4a}$-2,
即证-1-ln2-$\frac{1}{4a}$+ln(-$\frac{1}{a}$)≤-$\frac{3}{4a}$-2,即证-$\frac{1}{2}$(-$\frac{1}{a}$)+ln(-$\frac{1}{a}$)≤-1+ln2.
令t=-$\frac{1}{a}$,则t>0,问题转化为证明:-$\frac{1}{2}$t+lnt≤-1+ln2.…(*)
令g(t)=-$\frac{1}{2}$t+lnt,则g′(t)=-$\frac{1}{2}$+$\frac{1}{t}$,
令g′(t)=0可知t=2,则当0<t<2时g′(t)>0,当t>2时g′(t)<0,
所以y=g(t)在(0,2)上单调递增、在(2,+∞)上单调递减,
即g(t)≤g(2)=-$\frac{1}{2}$×2+ln2=-1+ln2,即(*)式成立,
所以当a<0时,f(x)≤-$\frac{3}{4a}$-2成立.
点评 本题考查利用导数研究函数的单调性,考查分类讨论的思想,考查转化能力,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
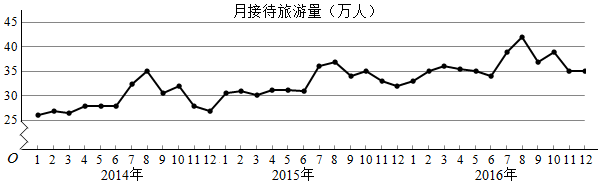
| A. | 月接待游客量逐月增加 | |
| B. | 年接待游客量逐年增加 | |
| C. | 各年的月接待游客量高峰期大致在7,8月 | |
| D. | 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-1,1] | C. | [0,4] | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | π | B. | $\frac{3π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1盏 | B. | 3盏 | C. | 5盏 | D. | 9盏 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com