
分析 求得切线方程,分别令x=0,求得B点坐标,当y=0时,求得A点坐标,根据三角形的面积公式,即可求得与两坐标轴围成的三角形面积为定值.
解答  解:证明:设曲线$y=\frac{1}{x}$上任意一点为P(x0,$\frac{1}{{x}_{0}}$),∵y′=-$\frac{1}{{x}^{2}}$,
解:证明:设曲线$y=\frac{1}{x}$上任意一点为P(x0,$\frac{1}{{x}_{0}}$),∵y′=-$\frac{1}{{x}^{2}}$,
∴在点P处切线的斜率k=-$\frac{1}{{x}_{0}^{2}}$,
∴在P点处的切线方程为y-$\frac{1}{{x}_{0}}$=-$\frac{1}{{x}_{0}^{2}}$(x-x0).
令x=0,得y=$\frac{1}{{x}_{0}}$+$\frac{1}{{x}_{0}}$=$\frac{2}{{x}_{0}}$,则B(0,$\frac{2}{{x}_{0}}$)
令y=0,得x=x0+x02×$\frac{1}{{x}_{0}}$=2x0,C(2x0,0),
∴S△=$\frac{1}{2}$|x|•|y|=2.
故三角形面积为定值2.
过P处的切线与与两坐标轴围成的三角形面积为定值2.
点评 本题考查利用导数求函数的切线方程,考查计算能力,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
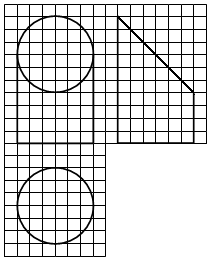 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )| A. | 90π | B. | 63π | C. | 42π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | b<c<a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com