
分析 (1)将P(1,e)代入函数表达式,求出a的值,根据函数的奇偶性,求出b的值即可;
(2)问题转化为$k<\frac{e^x}{x},x∈({0,+∞})$,记$h(x)=\frac{e^x}{x},x∈({0,+∞})$,根据函数的单调性求出k的范围即可;
(3)求出x1•x2的表达式,得到${x_1}{x_2}=tx_1^2=t{({\frac{lnt}{t-1}})^2}$,…[(13分)]要证x1x2<1,即证$\sqrt{t}\frac{lnt}{t-1}<1$,令$μ=\sqrt{t}({μ>1})$,问题转化为2μlnμ<μ2-1⇒2μlnμ-μ2+1<0,令φ(μ)=2μlnμ-μ2+1(μ>1),根据函数的单调性证明即可.
解答 解:(1)∵f(1)=e,
∴${e^{2a}}=e⇒a=\frac{1}{2}$,…[(2分)],
∵g(x)=kx+b为奇函数,
∴b=0;…[(4分)]
(2)由(1)知f(x)=ex,g(x)=kx,…[(5分)]
因为y轴右侧图象C恒在l的上方,
所以当x>0时,ex>kx恒成立,…[(6分)]
∴$k<\frac{e^x}{x},x∈({0,+∞})$,…[(7分)]
记$h(x)=\frac{e^x}{x},x∈({0,+∞})$,则$h'(x)=\frac{x-1}{x^2}{e^x}$,
由h'(x)>0⇒x∈(1,+∞),
∴h(x)在(0,1]单调减,在[1,+∞)单调增,…[(8分)]
h(x)∈[e,+∞),
∴k∈(-∞,e),…[(10分)]
证明:(3)由(2)知0<x1<1<x2,设x2=tx1(t>1),…[(11分)]
∵${e^{x_1}}=k{x_1},{e^{x_2}}=k{x_2}$,
∴${e^{{x_2}-{x_1}}}=\frac{x_2}{x_1}⇒{e^{({t-1}){x_1}}}=t$,…[(12分)]
$({t-1}){x_1}=lnt⇒{x_1}=\frac{lnt}{t-1}$,
∴${x_1}{x_2}=tx_1^2=t{({\frac{lnt}{t-1}})^2}$,…[(13分)]
要证x1x2<1,即证$\sqrt{t}\frac{lnt}{t-1}<1$,令$μ=\sqrt{t}({μ>1})$,
即证2μlnμ<μ2-1⇒2μlnμ-μ2+1<0,
令φ(μ)=2μlnμ-μ2+1(μ>1),即证φ(μ)<0,
$φ'(μ)=2lnμ-2μ+2⇒φ''(μ)=\frac{2}{μ}-2=\frac{{2({1-μ})}}{μ}$,
∵μ>1,∴φ''(μ)<0,
∴φ'(μ)在(1,+∞)上单调减,
∴φ'(μ)<φ'(1)=0,
∴φ(μ)在(1,+∞)上单调减,
∴φ(μ)<φ(1)=0,
所以x1•x2<1…[(16分)]
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及不等式的证明,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{43}{128}$ | B. | $\frac{43}{64}$ | C. | $\frac{13}{128}$ | D. | $\frac{13}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
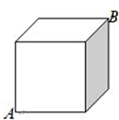 如图是边长为1的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请问蜘蛛从A到B正方体表面爬行的最短路程为( )
如图是边长为1的正方体,有一蜘蛛潜伏在A处,B处有一小虫被蜘蛛网粘住,请问蜘蛛从A到B正方体表面爬行的最短路程为( )| A. | 3 | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}$-y2=1 | B. | $\frac{x^2}{4}$-$\frac{y^2}{3}$=1 | C. | $\frac{x^2}{4}$-y2=1 | D. | $\frac{x^2}{8}$-$\frac{y^2}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com