
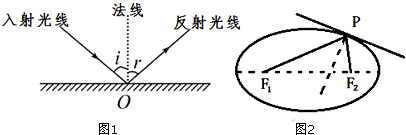
分析 (1)桌球第一次与球桌边缘的接触点可能椭圆长轴的两个端点及这两个端点外的任一点三种情况,即可得出结论;
(2)①求出点A,B的坐标均满足方程,即可证明直线lAB恒过一定点;
②由(2)的结论知:椭圆C在P(x0,y0)处的切线l的方程为$\frac{{{x_0}x}}{4}+{y_0}y=1$,由事实现象(2)知:直线PI⊥l,即可得出结论.
解答 解:(1)记$c=\sqrt{{a^2}-{b^2}}$,
因为桌球第一次与球桌边缘的接触点可能椭圆长轴的两个端点及这两个端点外的任一点三种情况,
所以S=2(a-c)或S=2(a+c)或S=4a;[(4分)]
(2)①设$M({\frac{{4\sqrt{3}}}{3},t})({t∈R}),A({{x_1},{y_1}}),B({{x_2},{y_2}})$,则…[(5分)]${l_{MA}}:\frac{{{x_1}x}}{4}+{y_1}y=1,{l_{MB}}:\frac{{{x_2}x}}{4}+{y_2}y=1$,…[(6分)]
代入$M({\frac{{4\sqrt{3}}}{3},t})$,得${l_{MA}}:\frac{{\sqrt{3}}}{3}{x_1}+t{y_1}=1,{l_{MB}}:\frac{{\sqrt{3}}}{3}{x_2}+t{y_2}=1$,…[(7分)]
则点A,B的坐标均满足方程$\frac{{\sqrt{3}}}{3}x+ty=1,即{l_{AB}}:\frac{{\sqrt{3}}}{3}x+ty-1=0$,…[(9分)]
所以,直线AB恒过定点$F({\sqrt{3},0})$;…[(10分)]
②由(2)的结论知:椭圆C在P(x0,y0)处的切线l的方程为$\frac{{{x_0}x}}{4}+{y_0}y=1$,…[(11分)]
由事实现象(2)知:直线PI⊥l,
∴${l_{PI}}:y=\frac{{4{y_0}}}{x_0}x-3{y_0}$…[(13分)]
令y=0,得点N的横坐标为${x_N}=\frac{{3{x_0}}}{4}$,…[(5分)]
∵x0∈(0,2),
∴${x_N}∈({0,\frac{3}{2}})$.…[(16分)]
点评 本题考查直线过定点,考查直线与椭圆的位置关系,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C,D是⊙O上的点,AD是∠BAC的平分线,过点D作DE⊥AC,交AC的延长线于点E.
如图,AB是⊙O的直径,C,D是⊙O上的点,AD是∠BAC的平分线,过点D作DE⊥AC,交AC的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
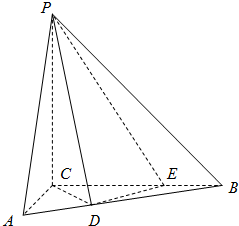 三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4
三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com