
 某观测站C在城A的南偏西20°的方向上,由A城出发有一条公路,走向是南偏东25°,在C处测得距C为14千米的公路上B处有一人正沿公路向A城走去,走了6千米后,到达D处,此时C、D间距离为10千米,
某观测站C在城A的南偏西20°的方向上,由A城出发有一条公路,走向是南偏东25°,在C处测得距C为14千米的公路上B处有一人正沿公路向A城走去,走了6千米后,到达D处,此时C、D间距离为10千米,分析 求出cos∠BDC,进而可得∠ADC,在△ACD中,由正弦定理求得AC,AD,答案可得.
解答 解:(1)由已知得CD=10,BC=14,BD=6,
在△BCD中,由余弦定理得 cos∠BDC=$\frac{100+36-196}{2×10×6}$=-$\frac{1}{2}$,
∴∠BDC=120°,
∴∠ADC=60°.
在△ACD中,由正弦定理得$\frac{10}{sin45°}=\frac{AC}{sin60°}$=$\frac{AD}{sin75°}$,∴AC=5$\sqrt{6}$千米,AD=5($\sqrt{3}+1$)千米;
(2)由(1)可得还需走5($\sqrt{3}+1$)千米到达A城.
点评 本题主要考查了解三角形的实际应用.解题的关键是利用正弦定理,利用边和角的关系求得答案.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
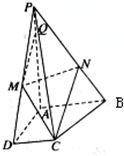 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥平面ABCD.点Q在PA上,且PA=4PQ=4.∠CDA=∠BAD=$\frac{π}{2}$,AB=2,CD=1,AD=$\sqrt{2}$.M,N分别为PD,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,PA⊥平面ABCD.点Q在PA上,且PA=4PQ=4.∠CDA=∠BAD=$\frac{π}{2}$,AB=2,CD=1,AD=$\sqrt{2}$.M,N分别为PD,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
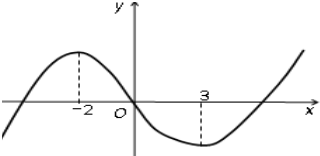
| A. | $({\frac{1}{2},+∞})$ | B. | $({-∞,\frac{1}{2}})$ | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
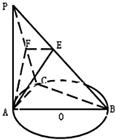 如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:
如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,ABCD为平行四边形,BCEF是边长为1的正方形,$BF⊥BA,∠DAB=\frac{π}{3},AB=2AD$.
如图,ABCD为平行四边形,BCEF是边长为1的正方形,$BF⊥BA,∠DAB=\frac{π}{3},AB=2AD$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com