
���� ��1�������¼�����n=107�����Ƚ������Ļ����¼�����m=9+9=18���ɴ���������ö��Ƚ��ĸ��ʣ�
��2���������Ƚ������Ͻ��������һ�Ƚ�����ö��Ƚ���������Ƚ�3��������ɴ�������������Ƚ������Ͻ��ĸ��ʣ�
��� �⣺��1��ij�ֲ�Ʊ��Ͷע������7λ������ɣ�ÿλ���־�Ϊ0��9��10�������е�����1����
��ҡ�ŵó�1��7λ������λ��Ϊ0��Ϊ�н��ţ������¼�����n=107��
��6λ�����������н��ŵ���Ӧ��λ�ϵ�������ͬ���ö��Ƚ���
����Ƚ������Ļ����¼�����m=9+9=18��
�����ö��Ƚ��ĸ���p1=$\frac{18}{{{{10}^7}}}=\frac{9}{{5��{{10}^6}}}$������6�֣�
��2���������Ƚ������Ͻ��������һ�Ƚ�����ö��Ƚ���������Ƚ�3�������
���������Ƚ������Ͻ��ĸ���p2=$\frac{1+18+261}{{{{10}^7}}}=\frac{7}{{25��{{10}^4}}}$������16�֣�
���� ���⿼����ʵȻ���֪ʶ���������ݴ�������������������������鼯��˼�룬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{9}$ | B�� | $\frac{8}{9}$ | C�� | $\frac{{4\sqrt{2}}}{9}$ | D�� | $\frac{{2\sqrt{2}}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ��ӱ�ʡ�߶����ϵ�һ���¿���ѧ�Ծ��������棩 ���ͣ������
��֪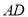 ��
��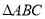 ��
��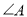 �Ľ�ƽ���ߣ���
�Ľ�ƽ���ߣ���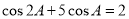 ��
��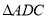 ��
��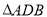 �����֮��Ϊ1:2��
�����֮��Ϊ1:2��
��1����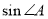 ��ֵ��
��ֵ��
��2����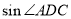 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ֲ���� | B�� | ��ǩ�� | C�� | ��������� | D�� | ϵͳ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� | [60��70] |
| Ƶ�� | 2 | 3 | 4 | 5 | 4 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 18 | B�� | 24 | C�� | 30 | D�� | 32 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{8\sqrt{3}}{3}$ | B�� | 3$\sqrt{3}$ | C�� | $\frac{7\sqrt{3}}{2}$ | D�� | 4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com