
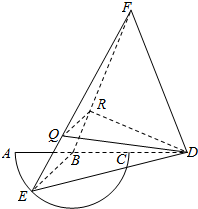
 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.分析 (Ⅰ)要证明EB⊥FD,我们可以转化为证明EB⊥平面BDF,证明EB⊥BF,结合线面垂直的判断定理和定义,不难给出结论.
(Ⅱ)要求平面BED与平面RQD所成二面角的正弦值,关键是要根据二面角的定义,先求出二面角的平面角,过D作HD∥QR,∠RDB是平面BED与平面RQD所成二面角的平面角,解三角形RDB即可得到结论.
解答 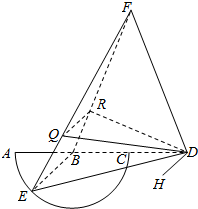 (Ⅰ)证明:∵E为弧AC的中点,AB=BC,AC为直径,∴EB⊥AD.
(Ⅰ)证明:∵E为弧AC的中点,AB=BC,AC为直径,∴EB⊥AD.
∵$E{F^2}=6{a^2}={(\sqrt{5}a)^2}+{a^2}=B{F^2}+B{E^2}$,∴EB⊥FB.
∵BF∩BD=B,∴EB⊥平面BDF.
∵FD?平面BDF,∴EB⊥FD.…4分
(Ⅱ)解:过D作HD∥QR.
∵$\overrightarrow{FQ}=λ\overrightarrow{FE},\overrightarrow{FR}=λ\overrightarrow{FB}$,∴QR∥EB.∴HD∥EB.
∵D∈平面BED∩平面RQD,
∴HD为平面BED与平面RQD的交线.
∵BD,RD?平面BDF,EB⊥平面BDF,
∴HD⊥BD,HD⊥RD.
∴∠RDB为平面BED与平面RQD所成二面角的平面角.
∵△BRD是直角三角形,∴$sin∠BDR=\frac{BR}{BD}=\frac{{\frac{2}{5}\sqrt{5}a}}{2a}=\frac{{\sqrt{5}}}{5}$.…6分
点评 本题考查线面垂直的判定与性质,考查二面角的平面角,考查学生分析解决问题的能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com