
(5分)方程(1﹣k)x2+(3﹣k2)y2=4(k∈R),当k= 时,表示圆;当k∈ 时,表示椭圆;当k∈ 时,表示双曲线;当k= 时,表示两条直线.
﹣1,(﹣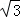 ,﹣1)∪(﹣1,1),(﹣∞,﹣
,﹣1)∪(﹣1,1),(﹣∞,﹣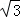 )∪(1,
)∪(1,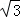 ),1或﹣
),1或﹣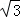 .
.
【解析】
试题分析:根据方程表示的曲线方程的特点,即可得到k的范围:方程表示圆?1﹣k=3﹣k2>0,方程表示椭圆?1﹣k>0,且3﹣k2>0,且1﹣k≠3﹣k2,方程表示双曲线?(1﹣k)(3﹣k2)<0,方程表示两条直线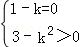
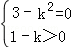 ,分别解出它们即可.
,分别解出它们即可.
【解析】
由于方程(1﹣k)x2+(3﹣k2)y2=4(k∈R),
则方程表示圆?1﹣k=3﹣k2>0,?k=﹣1或k=2(舍去);
方程表示椭圆?1﹣k>0,且3﹣k2>0,且1﹣k≠3﹣k2,
?k<1且﹣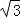 <k<
<k<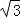 ,且k≠2且k≠﹣1.?﹣
,且k≠2且k≠﹣1.?﹣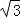 <k<1且k≠﹣1;
<k<1且k≠﹣1;
方程表示双曲线?(1﹣k)(3﹣k2)<0?k<﹣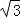 或1<k<
或1<k<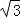 ;
;
方程表示两条直线?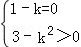
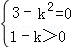 ?k=1或k=﹣
?k=1或k=﹣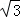 .
.
故答案为:﹣1,(﹣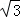 ,﹣1)∪(﹣1,1),(﹣∞,﹣
,﹣1)∪(﹣1,1),(﹣∞,﹣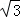 )∪(1,
)∪(1,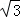 ),1或﹣
),1或﹣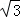 .
.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源:[同步]2014年北师大版必修三 1.6统计活动:结婚年龄的变化练习卷(解析版) 题型:选择题
(2014•重庆)某中学有高中生3500人,初中生1500人,为了解学生的学习情况,用分层抽样的方法从该校学生中抽取一个容量为n的样本,已知从高中生中抽取70人,则n为( )
A.100 B.150 C.200 D.250
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版必修三 1.1从普查到抽样练习卷(解析版) 题型:选择题
从2012名学生中选取50名组成参观团,若采用下面的方法选取:先用简单随机抽样从2012人中剔除12人,剩下的2000人再按系统抽样的方法进行.则每人入选的概率( )
A.不全相等 B.都相等,且为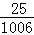
C.均不相等 D.都相等,且为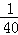
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)求一条渐近线方程是3x+4y=0,一个焦点是(5,0)的双曲线标准方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)(2010•广东)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列,则该椭圆的离心率是( )
A.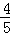 B.
B.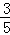 C.
C.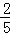 D.
D.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教B版选修2-1 第二章 圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)(2011•德阳二模)抛物线E:x2=2py(p>0)的焦点是离心率为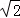 的双曲线:32y2﹣mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x﹣4上,则该正方形的面积是( )
的双曲线:32y2﹣mx2=1的一个焦点,正方形ABCD的两个顶点A、B在拋物线E上,C,D两点在直线y=x﹣4上,则该正方形的面积是( )
A.18或25 B.9或25 C.18或50 D.9或50
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.4练习卷(解析版) 题型:选择题
直角△ABC中,斜边AB上的高为CD,则( )
A.AB=CD2 B.AB≥2CD C.AB≤2CD D.AB2≤2CD
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:选择题
Ω是底面边长为1,高为2的正三棱柱被平面DEF截去几何体A1B1C1DEF后得到的几何体,其中D为线段AA1上异于A、A1的动点,E为线段BB1上异于B、B1的动点,F为线段CC1上异于C、C1的动点,且DF∥A1C1,则下列结论中不正确的是( )
A.DF⊥BB1 B.△DEF是锐角三角形
C.Ω可能是棱台 D.Ω可能是棱柱
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com