
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点, ![]() 为坐标原点,点
为坐标原点,点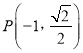 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)圆![]() 是以
是以![]() 为直径的圆,一直线
为直径的圆,一直线![]() 与圆
与圆![]() 相切,并与椭圆交于不同的两点
相切,并与椭圆交于不同的两点![]() 、
、![]() ,当
,当![]() ,且满足
,且满足![]() 时,求
时,求![]() 的面积
的面积![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】某企业生产 ![]() ,
, ![]() 两种产品,根据市场调查与预测,
两种产品,根据市场调查与预测, ![]() 产品的利润与投资关系如图(1)所示;
产品的利润与投资关系如图(1)所示; ![]() 产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资单位:万元).
产品的利润与投资的算术平方根成正比,其关系如图(2)所示(注:利润和投资单位:万元).
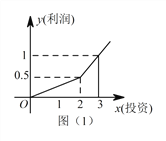
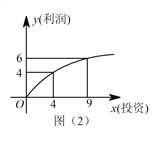
(1)分别将 ![]() ,
, ![]() 两种产品的利润表示为投资的函数关系式;
两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到 ![]() 万元资金,并将全部投入
万元资金,并将全部投入 ![]() ,
, ![]() 两种产品的生产.问怎样分配这
两种产品的生产.问怎样分配这 ![]() 万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年时红军长征胜利80周年,某市电视台举办纪念红军长征胜利80周年知识问答,宣传长征精神.首先在甲、乙、丙、丁四个不同的公园进行支持签名活动,其次在各公园签名的人中按分层抽样的方式抽取10名幸运之星,每人获得一个纪念品,其数据表格如下:
公园 | 甲 | 乙 | 丙 | 丁 |
获得签名人数 | 45 | 60 | 30 | 15 |
(Ⅰ)求此活动中各公园幸运之星的人数;
(Ⅱ)从乙和丙公园的幸运之星中任选两人接受电视台记者的采访,求这两人均来自乙公园的概率;
(Ⅲ)电视台记者对乙公园的签名人进行了是否有兴趣研究“红军长征”历史的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过0.01的前提下认为有兴趣研究“红军长征”历史与性别有关.
临界值表:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
参考公式: 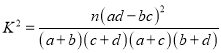 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题中是假命题的是
A. “昆虫都是6条腿,竹节虫是昆虫,所以竹节虫有6条腿”此推理属于演绎推理.
B. “在平面中,对于三条不同的直线![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,
, ![]() 则
则![]() ,将此结论放到空间中也成立” 此推理属于合情推理.
,将此结论放到空间中也成立” 此推理属于合情推理.
C. “![]() ”是“函数
”是“函数![]()
![]() 存在极值”的必要不充分条件.
存在极值”的必要不充分条件.
D. 若![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市需对某环城快速车道进行限速,为了调研该道路车速情况,于某个时段随机对![]() 辆车的速度进行取样,测量的车速制成如下条形图:
辆车的速度进行取样,测量的车速制成如下条形图:
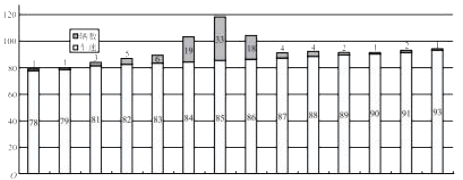
经计算:样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于
,以频率值作为概率的估计值.已知车速过慢与过快都被认为是需矫正速度,现规定车速小于![]() 或车速大于
或车速大于![]() 是需矫正速度.
是需矫正速度.
(1)从该快速车道上所有车辆中任取![]() 个,求该车辆是需矫正速度的概率;
个,求该车辆是需矫正速度的概率;
(2)从样本中任取![]() 个车辆,求这
个车辆,求这![]() 个车辆均是需矫正速度的概率;
个车辆均是需矫正速度的概率;
(3)从该快速车道上所有车辆中任取![]() 个,记其中是需矫正速度的个数为
个,记其中是需矫正速度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉著)一书中有关于三阶幻方的问题:将1, 2, 3, 4, 5, 6, 7, 8, 9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等 (如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是__________.
的方格中,使得每一行,每一列及对角线上的三个数的和都相等 (如图所示),我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是__________.
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的月固定成本为10(万元),每生产![]() 件,需另投入成本为
件,需另投入成本为![]() (万元).当月产量不足30件时,
(万元).当月产量不足30件时, ![]() (万元);当月产量不低于30件时,
(万元);当月产量不低于30件时, ![]() (万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(万元).因设备问题,该厂月生产量不超过50件.现已知此商品每件售价为5万元,且该厂每个月生产的商品都能当月全部销售完.
(1)写出月利润![]() (万元)关于月产量
(万元)关于月产量![]() (件)的函数解析式;
(件)的函数解析式;
(2)当月产量为多少件时,该厂所获月利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com