
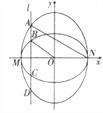
【题目】如图,已知椭圆![]() 的中心在原点
的中心在原点![]() ,长轴左、右端点
,长轴左、右端点![]() 、
、![]() 在
在![]() 轴上,椭圆
轴上,椭圆![]() 的短轴为
的短轴为![]() ,且
,且![]() 、
、![]() 的离心率都为
的离心率都为![]() ,直线
,直线![]() ,
, ![]() 与
与![]() 交于两点,与
交于两点,与![]() 交于两点,这四点纵坐标从大到小依次为
交于两点,这四点纵坐标从大到小依次为![]() 、
、![]() 、
、![]() 、
、![]() .
.
(1)设![]() ,求
,求![]() 与
与![]() 的比值;
的比值;
(2)若存在直线![]() ,使得
,使得![]() ,求两椭圆离心率
,求两椭圆离心率![]() 的取值范围.
的取值范围.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
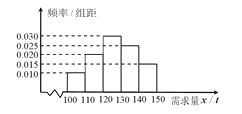
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,内角A,B,C的对边分别为a,b,c,且2asin B=![]() b.
b.
(1)求角A的大小; (2)若a=6,b+c=8,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为2,且函数
的短轴长为2,且函数![]() 的图象与椭圆
的图象与椭圆![]() 仅有两个公共点,过原点的直线
仅有两个公共点,过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 为线段
为线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 的一个公共点,求
的一个公共点,求![]() 面积的最小值,并求此时直线
面积的最小值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,
两点, ![]() 为
为![]() ,
, ![]() 的中点.
的中点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 所在的直线方程.
所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中, ![]() ,
, ![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻转成
翻转成![]() .若
.若![]() 为线段
为线段![]() 的中点,则在
的中点,则在![]() 翻折过程中:
翻折过程中:

①![]() 是定值;②点
是定值;②点![]() 在某个球面上运动;
在某个球面上运动;
③存在某个位置,使![]() ;④存在某个位置,使
;④存在某个位置,使![]() 平面
平面![]() .
.
其中正确的命题是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017 年省内某事业单位面向社会公开招骋工作人员,为保证公平竞争,报名者需要参加笔试和面试两部分,且要求笔试成绩必须大于或等于![]() 分的才有资格参加面试,
分的才有资格参加面试, ![]() 分以下(不含
分以下(不含![]() 分)则被淘汰,现有
分)则被淘汰,现有![]() 名竞骋者参加笔试,参加笔试的成绩按区间
名竞骋者参加笔试,参加笔试的成绩按区间![]() 分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为
分段,其频率分布直方图如图所示(频率分布直方图有污损),但是知道参加面试的人数为![]() ,且笔试成绩在
,且笔试成绩在![]() 的人数为
的人数为![]() .
.

(1)根据频率分布直方图,估算竞骋者参加笔试的平均成绩;
(2)若在面试过程中每人最多有![]() 次选题答题的机会,累计答对
次选题答题的机会,累计答对![]() 题或答错
题或答错![]() 题, 答对
题, 答对![]() 题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为
题者方可参加复赛,已知面试者甲答对每一个问题的概率都相同,并且相互之间没有影响,若他连续三次答题中答对一次的概率为![]() ,求面试者甲答题个数
,求面试者甲答题个数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() ,定点
,定点![]() (常数
(常数![]() )的直线
)的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(1)若点![]() 的坐标为
的坐标为![]() ,求证:
,求证: ![]()
(2)若![]() ,以
,以![]() 为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
为直径的圆的位置是否恒过一定点?若存在,求出这个定点,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com