
【题目】如图,在矩形ABCD中,AB=8,BC=4,E为DC边的中点,沿AE将△ADE折起,在折起过程中,有几个正确( )
①ED⊥平面ACD ②CD⊥平面BED ③BD⊥平面ACD ④AD⊥平面BED.
A.1个
B.2个
C.3个
D.4个
【答案】A
【解析】解:∵在矩形ABCD中,AB=8,BC=4,E为DC边的中点,
∴在折起过程中,D点在平面BCE上的投影如右图.
∵DE与AC所成角不能为直角,
∴DE不会垂直于平面ACD,故①错误;
只有D点投影位于O2位置时,即平面AED与平面AEB重合时,
才有BE⊥CD,此时CD不垂直于平面AEBC,
故CD与平面BED不垂直,故②错误;
BD与AC所成角不能成直线,
∴BD不能垂直于平面ACD,故③错误;
∵AD⊥ED,并且在折起过程中,有AD⊥BC,
∴存在一个位置使AD⊥BE,
∴在折起过程中AD⊥平面BED,故④正确.
故选:A.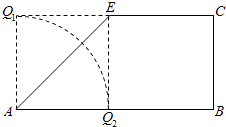
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 优等生题库系列答案
优等生题库系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】所谓正三棱锥,指的是底面为正三角形,顶点在底面上的射影为底面三角形中心的三棱锥,在正三棱锥S﹣ABC中,M是SC的中点,且AM⊥SB,底面边长AB=2 ![]() ,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
,则正三棱锥S﹣ABC的体积为 , 其外接球的表面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 满足:(1)截
满足:(1)截![]() 轴所得弦长为2;(2)被
轴所得弦长为2;(2)被![]() 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为![]() .在满足条件(1)、(2)的所有圆中,圆心到直线
.在满足条件(1)、(2)的所有圆中,圆心到直线![]() 的距离最小的圆的方程为__________.
的距离最小的圆的方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及样本频率分布表如下:
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | ② |
[80,90) | ① | 0.24 |
[90,100] | 4 | 0.08 |
合计 | ③ | ④ |
(1)请把给出的样本频率分布表中的空格都填上;
(2)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |
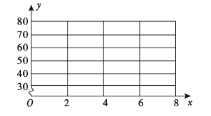
(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式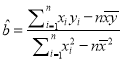 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2 ![]() 和4
和4 ![]() ,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
,M、N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最小值是1;
其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知几何体A﹣BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形. 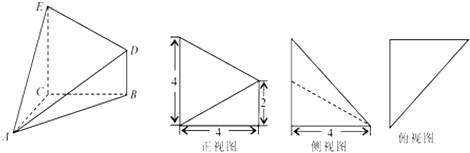
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 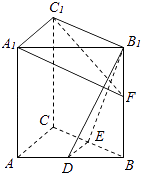
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com