
【题目】已知二元一次不等式组 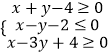 所表示的平面区域为M,若M与圆(x﹣4)2+(y﹣1)2=a(a>0)至少有两个公共点,则实数a的取值范围是( )
所表示的平面区域为M,若M与圆(x﹣4)2+(y﹣1)2=a(a>0)至少有两个公共点,则实数a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取100件样本,测量这些样本的一项质量指标值,由测量结果得如下频数分布表:
质量指标 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125] |
频数 | 6 | 26 | 38 | 22 | 8 |
则样本的该项质量指标值落在[105,125]上的频率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面是正方形,SA⊥底面ABCD,E是SC上一点. 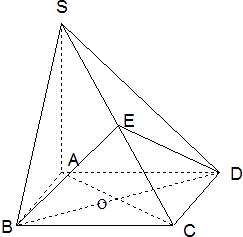
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
(3)设SA=4,AB=2,当OE丄SC时,求二面角E﹣BD﹣C余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(0,+∞)上的函数,当x>1时,f(x)>0,且满足 ![]() .
.
(1)求f(1)的值;
(2)判断并证明函数的单调性;
(3)若f(2)=1,解不等式 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=log2(1+x)+log2(1﹣x).
(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并加以说明;
(3)求f( ![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx,则函数g(x)=f(x)﹣f′(x)的零点所在的区间是( )
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com