
【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 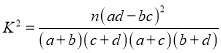 )
)
【答案】(1)表格祥见解析;(2)有,理由祥见解析;(3)![]() .
.
【解析】试题分析:(1)根据全部50人中随机抽取1人看营养说明的学生的概率为![]() ,做出看营养说明的人数,这样用总人数减去看营养说明的人数,剩下的是不看的,根据所给的另外两个数字,填上所有数字.
,做出看营养说明的人数,这样用总人数减去看营养说明的人数,剩下的是不看的,根据所给的另外两个数字,填上所有数字.
(2)根据列联表所给的数据,代入求观测值的公式,把观测值同临界值进行比较,得到有99.5%的把握说看营养说明与性别有关.
(3)利用列举法,求出基本事件的个数,即可求出正好抽到一男一女的概率.
试题解析:(1)设常喝碳酸饮料肥胖的学生有![]() 人,
人, ![]() ,
, ![]()
常喝 | 不常喝 | 合计 | |
肥胖 | 6 | 2 | 8 |
不胖 | 4 | 18 | 22 |
合计 | 10 | 20 | 30 |
(2)由已知数据可求得: ![]() ,
,
因此有99.5%的把握认为肥胖与常喝碳酸饮料有关.
(3)设其他工作人员为丙和丁,4人分组的所有情况如下表
小组 | 1 | 2 | 3 | 4 | 5 | 6 |
收集数据 | 甲乙 | 甲丙 | 甲丁 | 乙丙 | 乙丁 | 丙丁 |
处理数据 | 丙丁 | 乙丁 | 乙丙 | 甲丁 | 甲丙 | 甲乙 |
分组的情况总有6中,工作人员甲 负责收集数据且工作人员乙负责处理数据占两种,
所以工作人员甲负责收集数据且工作人员处理数据的概率是![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
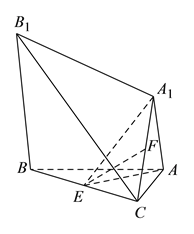
【题目】.某几何体如图所示, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是边长为
是边长为![]() 的正三角形,
的正三角形, ![]() ,
, ![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(I)求证: ![]() 平面
平面![]() .
.
(II)求证:平面![]() 平面
平面![]() .
.
(III)求该几何体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,过直线
的中点,过直线![]() ,
,![]() 的平面分别与棱
的平面分别与棱![]() 、
、![]() 交于
交于![]() ,
,![]() ,设
,设![]() ,
,![]() ,给出以下四个命题:
,给出以下四个命题:
①平面![]() 平面
平面![]() ;
;
②当且仅当![]() 时,四边形
时,四边形![]() 的面积最小;
的面积最小;
③四边形![]() 周长
周长![]() ,
,![]() 是单调函数;
是单调函数;
④四棱锥![]() 的体积
的体积![]() 为常函数;
为常函数;
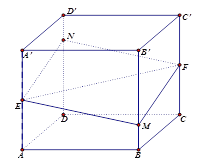
以上命题中假命题的序号为( ).
A. ①④ B. ② C. ③ D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com