
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{10}$ |
分析 可画出图形,并设$∠OAD=θ(0≤θ≤\frac{π}{2})$,这样便可求出点B,C的坐标,进而得出向量$\overrightarrow{OB},\overrightarrow{OC}$的坐标,从而求出$\overrightarrow{OB}+\overrightarrow{OC}$的坐标,这样即可求得$|\overrightarrow{OB}+\overrightarrow{OC}|=\sqrt{5+4sin2θ}$,从而可得出该最大值.
解答 解:如图,令∠OAD=θ,$(0≤θ≤\frac{π}{2})$,由于AD=1,
故0A=cosθ,OD=sinθ;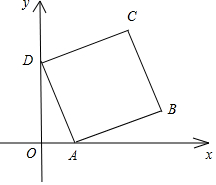 ∴$B(cosθ+cos(\frac{π}{2}-θ),sin(\frac{π}{2}-θ))$,
∴$B(cosθ+cos(\frac{π}{2}-θ),sin(\frac{π}{2}-θ))$,
C(sinθ,sinθ+cosθ);
∴$\overrightarrow{OB}=(cosθ+sinθ,cosθ)$,$\overrightarrow{OC}=(sinθ,sinθ+cosθ)$;
∴$\overrightarrow{OB}+\overrightarrow{OC}=(2sinθ+cosθ,sinθ+2cosθ)$;
∴$|\overrightarrow{OB}+\overrightarrow{OC}|=\sqrt{(2sinθ+cosθ)^{2}+(sinθ+2cosθ)^{2}}$
=$\sqrt{5+4sin2θ}$;
∴$2θ=\frac{π}{2}$时,$|\overrightarrow{OB}+\overrightarrow{OC}|$的最大值为3.
故选C.
点评 考查通过坐标解决向量问题的方法,能求平面上点的坐标,向量坐标的加法运算,根据向量坐标可求向量的长度.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{6}$ | B. | $\frac{20}{6}$ | C. | $\frac{23}{6}$ | D. | $\frac{26}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
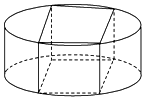 将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.
将一个底面圆的直径为2、高为1的圆柱截成一个长方体,如图所示,设这个长方体底面的一条边长为x、对角线长为2,底面的面积为A.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$.
已知函数f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若¬p:?x∈R,x2+x+1≥0 | B. | p为假命题 | ||
| C. | p∨¬p为假命题 | D. | ¬p为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在同一平面内,点P位于两平行直线l1、l2两侧,且P到l1,l2的距离分别为1,3,点M,N分别在l1,l2上,|$\overrightarrow{PM}$+$\overrightarrow{PN}$|=8,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最大值为( )
如图,在同一平面内,点P位于两平行直线l1、l2两侧,且P到l1,l2的距离分别为1,3,点M,N分别在l1,l2上,|$\overrightarrow{PM}$+$\overrightarrow{PN}$|=8,则$\overrightarrow{PM}$•$\overrightarrow{PN}$的最大值为( )| A. | 15 | B. | 12 | C. | 10 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com