
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由椭圆及双曲线的定义,求得|PF1|=$\sqrt{a}$+$\sqrt{b}$,|PF2|=$\sqrt{a}$-$\sqrt{b}$,由a-1=b+1,求得a-b=2,利用余弦定理求得cos∠F1PF2=0,则∠F1PF2=90°,根据三角形的面积公式求得△PF1F2的面积.
解答 解:由题意,|PF1|-|PF2|=2$\sqrt{b}$,|PF1|+|PF2|=2$\sqrt{a}$,
∴|PF1|=$\sqrt{a}$+$\sqrt{b}$,|PF2|=$\sqrt{a}$-$\sqrt{b}$,
∵椭圆$\frac{{x}^{2}}{a}$+y2=1与双曲线$\frac{{y}^{2}}{b}$-y2=1有相同的焦点
∴a-1=b+1
∴a-b=2
∴cos∠F1PF2=$\frac{2b+2a-4(a-1)}{2(\sqrt{b}+\sqrt{a})(\sqrt{b}-\sqrt{a})}$=$\frac{2b+2a-4a+4}{2(a-b)}$=$\frac{0}{2×2}$=0
∴∠F1PF2=90°
∴△PF1F2的面积为$\frac{1}{2}$|PF1||PF2|=$\frac{1}{2}$(a-b)=1,
∴△PF1F2的面积1,
故选:D.
点评 本题考查椭圆、双曲线的定义,考查余弦定理的运用,考查三角形面积的计算,属于中档题.


科目:高中数学 来源: 题型:解答题
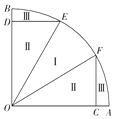 现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).
现有一个以OA、OB为半径的扇形池塘,在OA、OB上分别取点C、D,作DE∥OA、CF∥OB分别交弧AB于点E、F,且BD=AC,现用渔网沿着DE、EO、OF、FC将池塘分成如图所示的养殖区域.已知OA=1km,∠AOB=$\frac{π}{2}$,∠EOF=θ(0<θ<$\frac{π}{2}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用时间 | [0,2] | (2,4] | (4,6] |
| 女生人数 | 20 | 20 | z |
| 男生人数 | 20 | 40 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
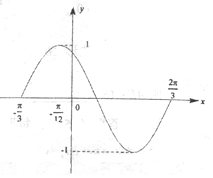 如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )
如图是函数y=Asin(ωx+φ)(x∈R)在区间[-$\frac{π}{3}$,$\frac{2π}{3}$]上的图象,为了得到这个函数的图象.只需将y=cosx(x∈R)的图象上的所有点( )| A. | 向左平移$\frac{π}{6}$个单位长度,再把所有点的横坐标扩大到原来的2倍 | |
| B. | 向左平移$\frac{π}{12}$个单位长度.再把所有点的横坐标扩大到原来的2倍 | |
| C. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{12}$个单位长度 | |
| D. | 把所有点的横坐标缩短到原来的$\frac{1}{2}$,再向左平移$\frac{π}{6}$个单位长度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com