
【题目】已知直线![]() :
:![]() ,若存在实数
,若存在实数![]() 使得一条曲线与直线
使得一条曲线与直线![]() 有两个不同的交点,且以这两个交点为端点的线段长度恰好等于
有两个不同的交点,且以这两个交点为端点的线段长度恰好等于![]() ,则称此曲线为直线
,则称此曲线为直线![]() 的“绝对曲线”.下面给出的四条曲线方程:
的“绝对曲线”.下面给出的四条曲线方程:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .
.
其中直线![]() 的“绝对曲线”的条数为( )
的“绝对曲线”的条数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
由y=ax+1﹣a=a(x﹣1)+1,可知直线l过点A(1,1).
对于①,y=﹣2|x﹣1|,图象是顶点为(1,0)的倒V型,而直线l过顶点A(1,1).所以直线l不会与曲线y=﹣2|x﹣1|有两个交点,不是直线l的“绝对曲线”;
对于②,(x﹣1)2+(y﹣1)2=1是以A为圆心,半径为1的圆,
所以直线l与圆总有两个交点,且距离为直径2,所以存在a=±2,使得圆(x﹣1)2+(y﹣1)2=1与直线l有两个不同的交点,且以这两个交点为端点的线段的长度恰好等于|a|.
所以圆(x﹣1)2+(y﹣1)2=1是直线l的“绝对曲线”;
对于③,将y=ax+1﹣a代入x2+3y2=4,
得(3a2+1)x2+6a(1﹣a)x+3(1﹣a)2﹣4=0.
x1+x2=![]() , x1x2=
, x1x2=![]() .
.
若直线l被椭圆截得的线段长度是|a|,
则![]()
化简得![]() .
.
令f(a)=![]() .
.
f(1)![]() ,f(3)
,f(3)![]() .
.
所以函数f(a)在(1,3)上存在零点,即方程![]() 有根.
有根.
而直线过椭圆上的定点(1,1),当a∈(1,3)时满足直线与椭圆相交.
故曲线x2+3y2=4是直线的“绝对曲线”.
对于④将y=ax+1﹣a代入![]() .
.
把直线y=ax+1-a代入y2=4x得a2x2+(2a-2a2-4)x+(1-a)2=0,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
若直线l被椭圆截得的弦长是|a|,
则a2=(1+a2)[(x1+x2)2-4x1x2]=(1+a2)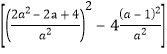
化为a6-16a2+16a-16=0,
令f(a)=a6-16a2+16a-16,而f(1)=-15<0,f(2)=16>0.
∴函数f(a)在区间(1,2)内有零点,即方程f(a)=0有实数根,当a∈(1,2)时,直线满足条件,即此函数的图象是“绝对曲线”.
综上可知:能满足题意的曲线有②③④.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 交
交![]() 于点
于点![]() .现将
.现将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到图2.
,得到图2.
(Ⅰ)在图2中,求证: ![]() ;
;
(Ⅱ)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在什么位置时,二面角
在什么位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间有5名工人其中初级工2人,中级工2人,高级工1人![]() 现从这5名工人中随机抽取2名.
现从这5名工人中随机抽取2名.
![]() Ⅰ
Ⅰ![]() 求被抽取的2名工人都是初级工的概率;
求被抽取的2名工人都是初级工的概率;
![]() Ⅱ
Ⅱ![]() 求被抽取的2名工人中没有中级工的概率.
求被抽取的2名工人中没有中级工的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B.
(Ⅰ)若∠APB=60°,试求点P的坐标;
(Ⅱ)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=![]() 时,求直线CD的方程.
时,求直线CD的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】省环保厅对![]() 、
、![]() 、
、![]() 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:
|
|
| |
优(个) | 28 |
|
|
良(个) | 32 | 30 |
|
已知在这180个数据中随机抽取一个,恰好抽到记录![]() 城市空气质量为优的数据的概率为0.2.
城市空气质量为优的数据的概率为0.2.
(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在![]() 城中应抽取的数据的个数;
城中应抽取的数据的个数;
(2)已知![]() ,
, ![]() ,求在
,求在![]() 城中空气质量为优的天数大于空气质量为良的天数的概率.
城中空气质量为优的天数大于空气质量为良的天数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 与圆
与圆![]() 的4个交点恰为一个正方形的4个顶点.
的4个交点恰为一个正方形的4个顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() 为椭圆
为椭圆![]() 的下顶点,
的下顶点, ![]() 为椭圆
为椭圆![]() 上与
上与![]() 不重合的两点,若直线
不重合的两点,若直线![]() 与直线
与直线![]() 的斜率之和为
的斜率之和为![]() ,试判断是否存在定点
,试判断是否存在定点![]() ,使得直线
,使得直线![]() 恒过点
恒过点![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家面包房根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图,如图231所示.
 图231
图231
将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
(1)求在未来连续3天里,有连续2天的日销售量都不低于100个且另1天的日销售量低于50个的概率;
(2)用X表示在未来3天里日销售量不低于100个的天数,求随机变量X的分布列,期望E(X)及方差D(X).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com