
【题目】如图1,在矩形ABCD中, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 交
交![]() 于点
于点![]() .现将
.现将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到图2.
,得到图2.
(Ⅰ)在图2中,求证: ![]() ;
;
(Ⅱ)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在什么位置时,二面角
在什么位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.

【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(1)先证明![]() ,再证明
,再证明![]() ,证明
,证明![]() 平面
平面![]() ,从而可得
,从而可得![]() ;
;
(2)建立直角坐标系,设![]() ,求出平面
,求出平面![]() 、平面
、平面![]() 的一个法向量,利用向量的夹角公式,结合二面角
的一个法向量,利用向量的夹角公式,结合二面角![]() 的余弦值为
的余弦值为![]() ,即可得出结论.
,即可得出结论.
试题解析:(Ⅰ)∵在矩形![]() 中,
中, ![]() ,
, ![]() ,
,
∴![]() , ∴
, ∴![]() 即
即![]() .
.
∴在图2中, ![]() ,
, ![]() .
.
又∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() , ∴
, ∴![]() ,
,
依题意, ![]() ∥
∥![]() 且
且![]() ,∴四边形
,∴四边形![]() 为平行四边形.
为平行四边形.
∴![]() ∥
∥![]() , ∴
, ∴![]() , 又∵
, 又∵![]() ,
,
∴![]() 平面
平面![]() , 又∵
, 又∵![]() 平面
平面![]() , ∴
, ∴![]() .
.
(Ⅱ)如图1,在![]() 中,
中, ![]() ,
, ![]() ,
,
∵![]() ∥
∥![]() ,
, ![]() ,∴
,∴![]() .
.
 如图,以点
如图,以点![]() 为原点建立平面直角坐标系,则
为原点建立平面直角坐标系,则
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() 为平面
为平面![]() 的法向量.
的法向量.
设![]() ,则
,则![]() ,
,
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则
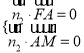 即
即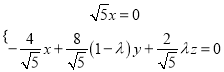 ,可取
,可取![]() ,
,
依题意,有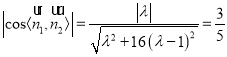 ,
,
整理得![]() ,即
,即![]() ,∴
,∴![]() ,
,
∴当点![]() 在线段
在线段![]() 的四等分点且
的四等分点且![]() 时,满足题意.
时,满足题意.


科目:高中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+a﹣2=0.
(1)当该方程的一个根为1时,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
(3)设该方程的两个实数根分别为x1 , x2 , 若2(x1+x2)+x1x2+10=0,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集合A={x|3≤x<9},B={x|1<x<7},C={x|x>m}.
(1)求A∪B;
(2)求(RA)∩B;
(3)若BC,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》.活动共有四关,若四关都闯过,则闯关成功,否则落水失败.设男生闯过一至四关的概率依次是![]() ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是![]() .
.
(Ⅰ)求男生甲闯关失败的概率;
(Ⅱ)设![]() 表示四人冲关小组闯关成功的人数,求随机变量
表示四人冲关小组闯关成功的人数,求随机变量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表:

(1)求关于的线性回归方程;
(2)利用(1)中的回归方程,当价格![]() 元
元![]() 时,日需求量
时,日需求量![]() 的预测值为多少?
的预测值为多少?
参考公式:线性归回方程: ![]() ,其中
,其中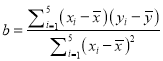 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5名男司机,4名女司机,需选派5人运货到吴忠.
(1)如果派3名男司机、2名女司机,共有多少种不同的选派方法?
(2)至少有两名男司机,共有多少种不同的选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)函数f(x)满足对任意的实数x,y都有f(xy)=f(x)+f(y),且f(4)=2,求f( ![]() )的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+
)的值; (Ⅱ)已知函数f(x)是定义在[﹣1,1]上的奇函数,且f(x)在[﹣1,1]上递增,求不等式f(x+ ![]() )+f(x﹣1)<0
)+f(x﹣1)<0
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com