
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
【答案】解:(Ⅰ)因为f(x)是奇函数,所以f(0)=0,
即 ![]()
又由f(1)=﹣f(﹣1)知 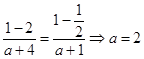 .
.
所以a=2,b=1.
经检验a=2,b=1时, ![]() 是奇函数.
是奇函数.
(Ⅱ)由(Ⅰ)知 ![]() ,
,
易知f(x)在(﹣∞,+∞)上为减函数.
又因为f(x)是奇函数,
所以f(t2﹣2t)+f(2t2﹣k)<0
等价于f(t2﹣2t)<﹣f(2t2﹣k)=f(k﹣2t2),
因为f(x)为减函数,由上式可得:t2﹣2t>k﹣2t2 .
即对一切t∈R有:3t2﹣2t﹣k>0,
从而判别式 ![]() .
.
所以k的取值范围是k<﹣ ![]()
【解析】(Ⅰ)利用奇函数定义,在f(﹣x)=﹣f(x)中的运用特殊值求a,b的值;
(Ⅱ)首先确定函数f(x)的单调性,然后结合奇函数的性质把不等式f(t2﹣2t)+f(2t2﹣k)<0转化为关于t的一元二次不等式,最后由一元二次不等式知识求出k的取值范围.
【考点精析】本题主要考查了函数的奇函数的相关知识点,需要掌握一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=—f(x),那么f(x)就叫做奇函数才能正确解答此题.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为an的一组正三角形AnBn﹣1Bn的底边Bn﹣1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为2的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则a的值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某学校用简单随机抽样方法抽取了100名同学,对其日均课外阅读时间(单位:分钟)进行调查,结果如下:
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
(i)求抽取的4位同学中既有男同学又有女同学的概率;
(ii)记抽取的“读书迷”中男生人数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C 的参数方程为 (
(![]() 为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
为参数),以直角坐标系原点O 为极点,x 轴正半轴为极轴建立极坐标系.
(Ⅰ)求曲线C 的极坐标方程;
(Ⅱ)设![]() ,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
,若l 1 、l2与曲线C 相交于异于原点的两点 A、B ,求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3. (Ⅰ)当a=﹣2时,求不等式f(x)<g(x)的解集;
(Ⅱ)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:设a,b∈R,则“a+b>4”是“a>2且b>2”的必要不充分条件;命题q:若 ![]() <0,则
<0,则 ![]() ,
, ![]() 夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
夹角为钝角,在命题①p∧q;②¬p∨¬q;③p∨¬q;④¬p∨q中,真命题是( )
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为A1B1 , CD的中点. 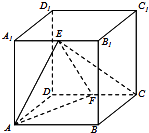
(1)求| ![]() |
|
(2)求直线EC与AF所成角的余弦值;
(3)求二面角E﹣AF﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com