
 已知一个几何体的三视图图图所示,求该几何体的外接球的表面积50π.
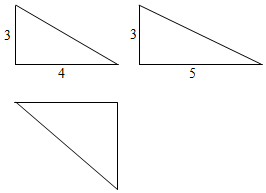
已知一个几何体的三视图图图所示,求该几何体的外接球的表面积50π. 分析 把三棱锥补成长方体,则长方体的对角线长等于其外接球的直径.
解答 解:由三视图可知该几何体为三棱锥,此三棱锥的底面为直角三角形,直角边长分别为5,4,且过底面的直角顶点的侧棱和底面垂直,该棱长为3,即棱锥的高为3,把三棱锥补成长方体,则长方体的对角线长等于其外接球的直径,
设球的半径为R,
∵长方体的对角线长$\sqrt{{3}^{2}+{4}^{2}+{5}^{2}}$=$\sqrt{50}$,
∴2R=$\sqrt{50}$,R=$\frac{\sqrt{50}}{2}$
∴外接球的表面积S=4πR2=50π.
故答案为:50π.
点评 本题考查球的内接体,球的表面积,考查空间想象能力,是基础题.


科目:高中数学 来源: 题型:解答题
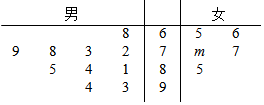 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
下列给出的赋值语句中正确的是( )
A.5 = M B.x =-x C.B=A=3 D.x +y = 7
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 车型 | A型 | B型 | C型 |
| 频数 | 20 | 20 | 40 |
| 单价x(元) | 800 | 820 | 840 | 850 | 880 | 900 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com