
分析 先证明n=2时,不等式成立,再假设n=k时,不等式成立,进而证明出n=k+1时,不等式也成立,即可得到结论.
解答 证明:(1)当n=2时,左边=1+$\frac{1}{\sqrt{2}}$=1+$\frac{\sqrt{2}}{2}$,右边=$\sqrt{2}$,1+$\frac{\sqrt{2}}{2}$>$\sqrt{2}$,所以不等式成立.
(2)假设n=k时不等式成立,即1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{k}}$>$\sqrt{k}$(k≥2,k∈N*),
那么当n=k+1时,1+$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{k}}$+$\frac{1}{\sqrt{k+1}}$>$\sqrt{k}$+$\frac{1}{\sqrt{k+1}}$=$\frac{\sqrt{k(k+1)}+1}{\sqrt{k+1}}$>$\frac{k+1}{\sqrt{k+1}}$=$\sqrt{k+1}$
即当n=k+1时,不等式也成立.
由(1)、(2)可知,对于任意n∈N+时,不等式成立.
点评 数学归纳法常常用来证明一个与自然数集N相关的性质,其步骤为:设P(n)是关于自然数n的命题,若1)(奠基) P(n)在n=1时成立;2)(归纳) 在P(k)(k为任意自然数)成立的假设下可以推出P(k+1)成立,则P(n)对一切自然数n都成立.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
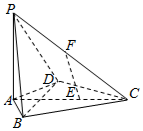 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{24}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com