
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
科目:高中数学 来源:2016-2017学年河北省高二8月月考数学试卷(解析版) 题型:选择题
给定下列四个命题:
①若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行;②若一个平面经过另一个平面的垂线,则这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,则一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( )
A.①和② B.②和③ C.③和④ D.②和④
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
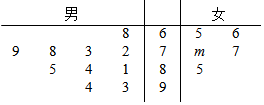 某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.
某校组织学生参加数学竞赛,共有15名学生获奖,其中10名男生和5名女生,其成绩如茎叶图所示(单位:分).规定:成绩在80分以上者为一等奖,80分以下者为二等奖,已知这5名女生的平均成绩为73.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com