
分析 (1)运用绝对值不等式的性质,注意等号成立的条件,即可求得最小值;
(2)根据a+b+c=2得到$\frac{a+b+c}{2}$=1,从而得到$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$=$\frac{a+b+c}{2a}$$+\frac{a+b+c}{2b}$+$\frac{a+b+c}{2c}$,根据级别不等式的性质求出最小值即可.
解答 解:(1)因为f(x)=|x+a|+|x-b|+c≥|(x+a)-(x-b)|+c=|a+b|+c,
当且仅当-a≤x≤b时,等号成立,
又a>0,b>0,所以|a+b|=a+b,
所以f(x)的最小值为a+b+c,
所以a+b+c=2;
(2)由(1)知a+b+c=2,
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$
=$\frac{a+b+c}{2a}$$+\frac{a+b+c}{2b}$+$\frac{a+b+c}{2c}$
=$\frac{1}{2}$$+\frac{b}{2a}$+$\frac{c}{2a}$+$\frac{a}{2b}$+$\frac{1}{2}$+$\frac{c}{2b}$+$\frac{a}{2c}$+$\frac{b}{2c}$+$\frac{1}{2}$
≥2$\sqrt{\frac{b}{2a}•\frac{a}{2b}}$+2$\sqrt{\frac{c}{2a}•\frac{a}{2c}}$+2$\sqrt{\frac{c}{2b}•\frac{b}{2c}}$+$\frac{3}{2}$
=1+1+1+$\frac{3}{2}$=$\frac{9}{2}$,
∴$\frac{1}{a}$+$\frac{1}{b}$+$\frac{1}{c}$的最小值是$\frac{9}{2}$.
点评 本题主要考查绝对值不等式、基本不等式的性质,是一道中档题.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源:2016-2017学年新疆库尔勒市高二上学期分班考试数学(理)试卷(解析版) 题型:填空题
已知两条不同直线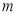 、
、 ,两个不同平面
,两个不同平面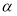 、
、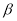 ,给出下列命题:
,给出下列命题:
①若 垂直于
垂直于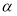 内的两条相交直线,则
内的两条相交直线,则 ⊥
⊥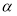 ;
;
②若 ∥
∥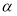 ,则
,则 平行于
平行于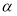 内的所有直线;
内的所有直线;
③若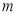
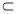
 ,
,
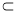
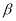 且
且 ⊥
⊥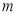 ,则
,则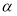 ⊥
⊥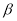 ;
;
④若
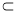
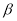 ,
,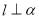 ,则
,则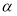 ⊥
⊥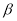 ;
;
⑤若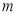
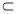
 ,
,
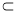
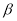 且
且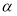 ∥
∥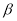 ,则
,则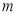 ∥
∥ ;
;
其中正确命题的序号是 .(把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,0) | B. | [-4,0] | C. | (-∞,-4)∪(0,+∞) | D. | (-∞,-4]∪[0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,cosx0+lnx0>1 | B. | ?x0∈R,cosx0+lnx0≥1 | ||
| C. | ?x∈R,cosx0+lnx0≥1 | D. | ?x∈R,cosx0+lnx0>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
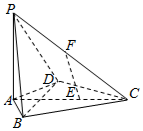 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com