
如图,已知四棱锥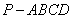 的底面为菱形,
的底面为菱形,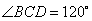 ,
,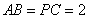 ,
,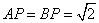 .
.
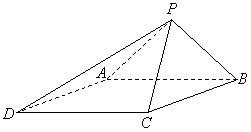

(Ⅰ)求证: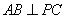 ;
;
(Ⅱ)求二面角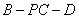 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
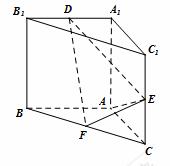
直三棱柱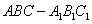 中,
中,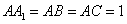 ,
,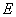 ,
,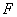
分别是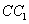 、
、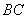 的中点,
的中点,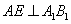 ,
, 为棱
为棱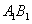 上的点.
上的点.
(1)证明: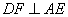 ;
;
(2)是否存在一点 ,使得平面
,使得平面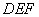 与平面
与平面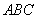 所成锐二面角的余弦值为
所成锐二面角的余弦值为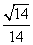 ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
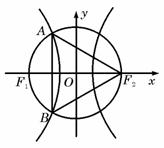
如图,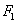 、
、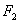 分别是双曲线
分别是双曲线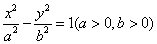 的两个焦点,以坐标原点
的两个焦点,以坐标原点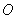 为圆心,
为圆心,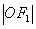 为半径的圆与该双曲线左支交于
为半径的圆与该双曲线左支交于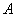 、
、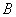 两点,若
两点,若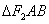 是等边三角形,则双曲线的离心率为 ( )
是等边三角形,则双曲线的离心率为 ( )
(A)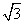 (B)
(B)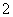 (C)
(C)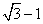 (D)
(D)
查看答案和解析>>
科目:高中数学 来源: 题型:
2014年11月,北京成功举办了亚太经合组织第二十二次领导人非正式会议,出席会议的有21个国家和地区的领导人或代表.其间组委会安排这21位领导人或代表合影留念,他们站成两排,前排11人,后排10人,中国领导人站在第一排正中间位置,美俄两国领导人站在与中国领导人相邻的两侧,如果对其他领导人或代表所站的位置不做要求,那么不同的排法共有 种(用排列组合表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数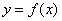 的定义域为
的定义域为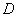 ,如果存在非零常数
,如果存在非零常数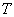 ,对于任意
,对于任意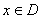 ,都有
,都有 ,则称函数
,则称函数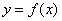 是“似周期函数”,非零常数
是“似周期函数”,非零常数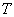 为函数
为函数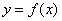 的“似周期”.现有下面四个关于“似周期函数”的命题:
的“似周期”.现有下面四个关于“似周期函数”的命题:
①如果“似周期函数”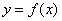 的“似周期”为-1,那么它是周期为2的周期函数;
的“似周期”为-1,那么它是周期为2的周期函数;
②函数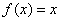 是“似周期函数”;
是“似周期函数”;
③函数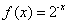 是“似周期函数”;
是“似周期函数”;
④如果函数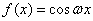 是“似周期函数”,那么“
是“似周期函数”,那么“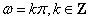 ”.
”.
其中是真命题的序号是 .(写出所有满足条件的命题序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
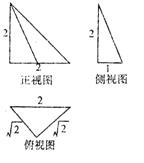
如图是一个空间几何体的三视图,该几何体的外接球的体积记为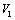 ,俯视图绕底边所在直线旋转一周形成的几何体的体积记为
,俯视图绕底边所在直线旋转一周形成的几何体的体积记为 ,则
,则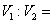 ( )
( )
(A)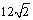 (B)
(B)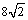 (C)
(C)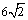 ( D)
( D)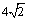
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com