Question

15．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（-x）（x＜0）}\\{{2}^{x}（x≥0）}\end{array}\right.$，若关于x的方程f²（x）-af（x）=0恰有三个不同的实数解，则实数a的取值范围为[1，+∞）．

Answer 1

分析 由题意作函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（-x）（x＜0）}\\{{2}^{x}（x≥0）}\end{array}\right.$的图象，由f²（x）-af（x）=0得f（x）=0或f（x）=a；从而解得．

解答 解：由题意作函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}（-x）（x＜0）}\\{{2}^{x}（x≥0）}\end{array}\right.$的图象如下，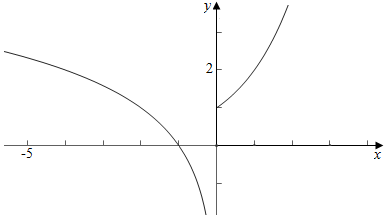
，
∵f²（x）-af（x）=0，
∴f（x）=0或f（x）=a；
∵f（x）=0有且只有一个解，
∴f（x）=a有且只有两个解，
故a∈[1，+∞）；
故答案为：[1，+∞）．

点评 本题考查了分段函数的应用及方程与函数的关系应用，同时考查了数形结合的思想应用．