
分析 对于①,根据奇数与偶数的定义,给出一个对应法则可验证①的正确性;
对②,根据复数的几何意义,可判断能否形成一一映射,来判断②是否正确;
对③,给出对应法则y=tan$\frac{π}{2}$x,可验证③的正确性.
解答 解:根据一一映射的定义,集合A={奇数}→B={偶数},不妨给出对应法则加1.则A→B是一一映射,故①正确;
对②设Z点的坐标(a,b),则Z点对应复数a+bi,a、b∈R,复合一一映射的定义,故②不正确;
对③,给出对应法则y=tan$\frac{π}{2}$x,对于A,B两集合可形成f:A→B的一一映射,则A、B具有相同的势;∴③正确.
故选:①③
点评 本题借助考查命题的真假判断,考查一一映射的定义,属于基础题型,考查考生对新定义题的理解与应用能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
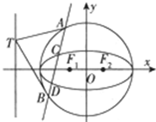 已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.
已知椭圆 C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点F1,F2,动点P在椭圆上,且使得∠F1PF2=90°的点P恰有两个,动点P到焦点F1的距离的最大值为2+$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com