
| A. | (2$\sqrt{2}$,+∞) | B. | (-1,2$\sqrt{2}$) | C. | (1,+∞) | D. | (-3,+∞) |
分析 函数f(x)=e|xex|是分段函数,通过求导分析得到函数f(x)在(0,+∞)上为增函数,在(-∞,-1)上为增函数,在(-1,0)上为减函数,求得函数f(x)在(-∞,0)上,当x=-1时有一个最大值1,则要使函数y=[f(x)]2+bf(x)-2恰有三个不同的零点,f(x)的值一个要在(0,1)内,一个在(-∞,0)内,然后运用二次函数的图象及二次方程根的关系列式求解b的取值范围.
解答 解:f(x)=e|xex|=$\left\{\begin{array}{l}{ex•{e}^{x},x≥0}\\{-ex•{e}^{x},x<0}\end{array}\right.$,
当x≥0时,f′(x)=ex+1(x+1)≥0恒成立,
∴f(x)在[0,+∞)上为增函数;
当x<0时,f′(x)=-ex+1(x+1),
由f′(x)=0,得x=-1,当x∈(-∞,-1)时,f′(x)=-ex+1(x+1)>0,f(x)为增函数,
当x∈(-1,0)时,f′(x)=-ex+1(x+1)<0,f(x)为减函数,
∴函数f(x)=e|xex|的极大值为f(-1)=1.
极小值为f(0)=0.
令f(x)=m,则m2+bm-2=0.
要使函数y=[f(x)]2+bf(x)-2恰有三个不同的零点,
则m2+bm-2=0一根小于0,另一根大于0小于1.
∴$\left\{\begin{array}{l}{-2<0}\\{{1}^{2}+b-2>0}\end{array}\right.$,
解得:b>1.
∴实数b的取值范围是(1,+∞).
故选:C.
点评 本题考查了根的存在性及根的个数的判断,考查了利用函数的导函数分析函数的单调性,考查了学生分析问题和解决问题的能力,解答此题的关键是分析出方程[f(x)]2+bf(x)-2=0有三个实数根时f(x)的取值情况,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x≤2} | B. | {x|-1<x<2} | C. | {x|x≥2或x≤-1} | D. | {x|x>2或x<-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
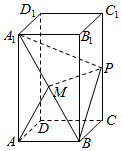 如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.
如图,正四棱柱ABCD-A1B1C1D1中,AD=1,D1D=2,点P为棱CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
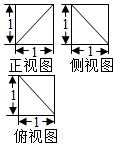
| A. | $\frac{2}{3}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 81 | B. | 171 | C. | 231 | D. | 371 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | -$\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com