
| ��ע��� | ��ע��� | �ܼ� | |
| �����û� | x | 5 | |
| Ů���û� | 7 | y | 8 |
| �ܼ� | 10 | 16 |
| P��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ������2��2��������д����x��y��ֵ������K2�����ٽ�ֵ�Ƚϣ������ж��Ƿ���95%���ϵİ�����Ϊ�Ա����ע��ߵ��йأ�
����������֪X�Ŀ���ȡֵΪ0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������������X�ķֲ��к���ѧ����EX��
��� �⣺����x=10-7=3��y=16-10-5=1��
K2=$\frac{16����3��1-7��5��^{2}}{10��6��8��8}$��4.27��3.841
����95%���ϵİ�����Ϊ�Ա����ע��ߵ��йأ�
����X��ʾѡ�е�ͬѧ��������ܴ�������10�ε�����������ȡ0��1��2��3��
P��X=0��$\frac{{C}_{3}^{0}{C}_{5}^{3}}{{C}_{8}^{3}}$=$\frac{10}{56}$��P��X=1��=$\frac{{C}_{3}^{1}{C}_{5}^{2}}{{C}_{8}^{3}}$=$\frac{30}{56}$��P��X=2��=$\frac{{C}_{3}^{2}{C}_{5}^{1}}{{C}_{8}^{3}}$=$\frac{15}{56}$��P��X=3��=$\frac{{C}_{3}^{3}}{{C}_{8}^{3}}$=$\frac{1}{56}$
X�ķֲ��У�
| X | 0 | 1 | 2 | 3 |
| P | $\frac{10}{56}$ | $\frac{30}{56}$ | $\frac{15}{56}$ | $\frac{1}{56}$ |
���� ���⿼������Լ���֪ʶ�����ã�������ɢ����������ķֲ��к������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
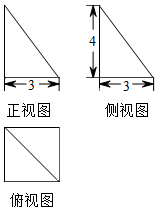
| A�� | 34�� | B�� | 35�� | C�� | 36�� | D�� | 17�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{3}{4}$ | B�� | $\frac{3}{4}$ | C�� | -$\frac{4}{3}$ | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com