
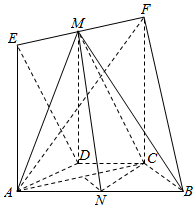
 如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.
如图,在几何体ABCDEF中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,FB=$\sqrt{10}$,M,N分别为EF,AB的中点.分析 (I)根据线面平行的判定定理进行证明即可;
(Ⅱ)建立空间直角坐标系,求平面的法向量,利用向量法进行求解.
解答 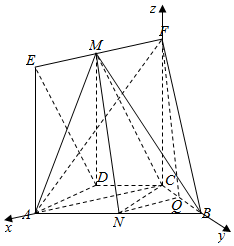 证明:(I)取BC的中点Q,连接NQ,FQ,则NQ=$\frac{1}{2}$AC,NQ∥AC.
证明:(I)取BC的中点Q,连接NQ,FQ,则NQ=$\frac{1}{2}$AC,NQ∥AC.
又MF=$\frac{1}{2}$AC,MF∥AC,所以MF=NQ,MF∥NQ,则四边形MNQF为平行四边形,即MN∥FQ.
∵PQ?平面FCB,MN?平面FCB,
∴MN∥平面.…5分
(Ⅱ)解:由AB∥CD,AD=DC=CB=1,∠ABC=60°可得,∠ACB=90°.AC=$\sqrt{3}$,BC=1,AB=2,
因为四边形ACFE为矩形,所以AC⊥平面FCB,
则∠AFC为直线AF与平面FCB所成的角,即∠AFC=30°,
∴FC=3.
∵FB=$\sqrt{10}$,∴FC⊥BC.
则可建立如图所示的空间直角坐标系C-xyz,
∴A($\sqrt{3}$,0,0).B(0,1,0),M($\frac{\sqrt{3}}{2}$,0,3),则$\overrightarrow{MA}$=($\frac{\sqrt{3}}{2}$,0,-3),$\overrightarrow{MB}$=(-$\frac{\sqrt{3}}{2}$,1,-3),
设$\overrightarrow{m}$=(x,y,z)为平面MAB的法向量,
则$\left\{\begin{array}{l}{\overrightarrow{MA}•\overrightarrow{m}=0}\\{\overrightarrow{MB}•\overrightarrow{m}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}x-3z=0}\\{-\frac{\sqrt{3}}{2}x+y-3z=0}\end{array}\right.$.
取x=2$\sqrt{3}$,则$\overrightarrow{m}$=(2$\sqrt{3}$,6,1)为平面MAB的一个法向量.
又$\overrightarrow{n}$=($\sqrt{3}$,0,0)为平面FCB的一个法向量,
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{2\sqrt{3}×\sqrt{3}}{7×\sqrt{3}}$=$\frac{2\sqrt{3}}{7}$.
则平面MAB与平面FCB所成角的余弦值为$\frac{2\sqrt{3}}{7}$.…12分
点评 本小题主要考查线面平行的判断和二面角的求解,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力,综合性较强,运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$ | D. | $\frac{2}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | ||
| C. | 相离 | D. | 以上三种均有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
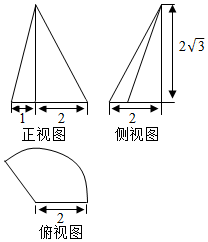 某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )
某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径为( )| A. | 4+$\frac{4π}{3}$ | B. | 6$\sqrt{3}$ | C. | 4+$\frac{2π}{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com