分析:(I)证明AB1垂直平面A1PD1内的两条相交直线:A1D1、A1P,即可证明AB1⊥平面A1PD1;
(II)设AB1∩A1P=E,过E作棱D1P的垂线EF,垂足为F,连接B1F,说明∠B1FE为二面角A1-D1P-B1的平面角,然后解三角形,求二面角A1-D1P-B1的正切值;
(III)点D到平面A1D1P的距离转化为点A到平面A1D1P的距离,然后求解即可.
解答: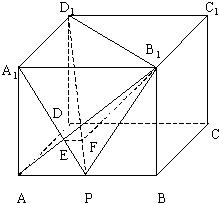
证明:(I)∵ABCD-A
1B
1C
1D
1是长方体
∴A
1D
1⊥平面A
1ABB
1且AB
1?平面A
1ABB
1
∴A
1D
1⊥AB
1∵
P为AB中点,A1A=AB=2,AP=1
在Rt△A1AP中,tanAA1P==在Rt△AB
1B中,tanB
1AB=
∴∠AA
1P=∠B
1AB
∵
在Rt△A1AP中,∠AA1P+∠A1PA=∴
∠B1AB+∠A1PA=∴A
1P⊥AB
1,又A
1D
1∩A
1P=A
1∴AB
1⊥平面A
1PD
1(5分)
解:(II)设AB
1∩A
1P=E,∵AB
1⊥平面A
1PD
1∴B
1E⊥平面A
1PD
1过E作棱D
1P的垂线EF,垂足为F,连接B
1F
则EF是B
1F在平面A
1PD
1内的射影,由三垂线定理得B
1F⊥D
1P
∴∠B
1FE为二面角A
1-D
1P-B
1的平面角
∵在Rt△AEP中,EP=AP•sinEAP=
=同理可得
B1E=又∵Rt△D
1A
1P∽Rt△EFP
∴
=∴
EF===在Rt△B
1EF中,
tanB1FE==4(10分)
(III)∵AD∥A
1D
1,且A
1D
1?平面A
1D
1P,AD?平面A
1D
1P
∴AD∥平面A
1D
1P
∴点D到平面A
1D
1P的距离等于点A到平面A
1D
1P的距离
∵AE⊥平面A
1D
1P
∴线段AE的长为点A到平面A
1D
1P的距离
∵
AE=∴点D到平面A
1D
1P的距离为
(14分)
点评:本题考查直线与平面垂直的判定,二面角的求法,考查空间想象能力,逻辑思维能力,是中档题.

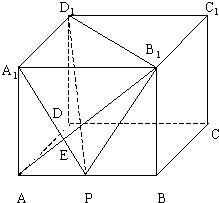 在长方体ABCD-A1B1C1D1中,点P为棱AB的中点,且AB=2,A1A=
在长方体ABCD-A1B1C1D1中,点P为棱AB的中点,且AB=2,A1A= 证明:(I)∵ABCD-A1B1C1D1是长方体
证明:(I)∵ABCD-A1B1C1D1是长方体

 (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.