【题目】下列命题中正确的是（ ）
A.过平面外一点作这个平面的垂面有且只有一个
B.过直线外一点作这条直线的平行平面有且只有一个
C.过直线外一点作这条直线的垂线有且只有一条
D.过平面外的一条斜线作这个平面的垂面有且只有一个
【答案】D
【解析】
A错误；如图长方体中，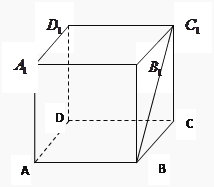
是平面ABCD外一点，平面
B错误；是直线AB外一点，
C错误；是直线AB外一点，
D正确；
是平面ABCD的一条斜线，平面
假设过做一个平面
则
这与是平面ABCD的一条斜线矛盾。
所以过平面外的一条斜线作这个平面的垂面有且只有一个。故选D
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识，掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点，以及对空间中直线与平面之间的位置关系的理解，了解直线在平面内—有无数个公共点；直线与平面相交—有且只有一个公共点；直线在平面平行—没有公共点．
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案科目：高中数学 来源： 题型：
【题目】国Ⅳ标准规定：轻型汽车的屡氧化物排放量不得超过80mg/km．根据这个标准，检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取5辆，对其氮氧化物的排放量进行检测，检测结果记录如表（单位：mg/km）
A | 85 | 80 | 85 | 60 | 90 |
B | 70 | x | 95 | y | 75 |
由于表格被污损，数据x，y看不清，统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等，方差也相等．
（1）求表格中x与y的值；
（2）从被检测的5辆B种型号的出租车中任取2辆，记“氮氧化物排放量超过80mg/km”的车辆数为X，求X=1时的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
（
）的离心率为
，以原点
为圆心，椭圆
的长半轴长为半径的圆与直线
相切.
（Ⅰ）求椭圆
的标准方程；
（Ⅱ）已知点
为动直线
与椭圆
的两个交点，问:在
轴上是否存在定点
,使得
为定值？若存在，试求出点
的坐标和定值；若不存在,请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
： 
，左焦点是
.
（1）若左焦点
与椭圆
的短轴的两个端点是正三角形的三个顶点，点
在椭圆
上.求椭圆
的方程；
（2）过原点且斜率为
的直线
与（1）中的椭圆
交于不同的两点
，设
，求四边形
的面积取得最大值时直线
的方程；
（3）过左焦点
的直线
交椭圆
于
两点，直线
交直线
于点
，其中
是常数，设
， 
，计算
的值（用
的代数式表示）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知二次函数
（Ⅰ）若函数在区间
上存在零点，求实数
的取值范围；
（Ⅱ）问：是否存在常数
，当
时， 
的值域为区间
，且
的长度为
．（说明：对于区间
，称
为区间长度）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】函数f（x）=
（cosx﹣sinx）sin（x+
）﹣2asinx+b（a＞0）．
（1）若b=1，且对任意
， 恒有f（x）＞0，求a的取值范围；
（2）若f（x）的最大值为1，最小值为﹣4，求实数a，b的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
