
分析 (I)B(ρ,θ+$\frac{π}{3}$),化为直角坐标:B$(ρcos(θ+\frac{π}{3}),ρsin(θ+\frac{π}{3}))$,利用|BM|=1,可得ρ2+4ρ$cos(θ+\frac{π}{3})$+3=0,展开把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$及其ρ2=x2+y2代入即可得出.
(II)x2+y2+2x-2$\sqrt{3}$y+3=0配方为:(x+1)2+$(y-\sqrt{3})^{2}$=1,可得圆心C,半径r.得出点P(-1,0)到圆心C的距离d.A(ρ,θ)化为直角坐标A(x,y).|OA|2+|MA|2=2[(x+1)2+y2]+2∈[2d2-1+2,2d2+1+2].
解答 解:(I)B(ρ,θ+$\frac{π}{3}$),化为直角坐标:B$(ρcos(θ+\frac{π}{3}),ρsin(θ+\frac{π}{3}))$,
∵|BM|=1,∴$\sqrt{[ρcos(θ+\frac{π}{3})+2]^{2}+[ρsin(θ+\frac{π}{3})]^{2}}$=1,化为:ρ2+4ρ$cos(θ+\frac{π}{3})$+3=0,展开:ρ2+$4ρ(\frac{1}{2}cosθ-\frac{\sqrt{3}}{2}sinθ)$+3=0,
化为直角坐标方程:x2+y2+2x-2$\sqrt{3}$y+3=0.
(II):x2+y2+2x-2$\sqrt{3}$y+3=0配方为:(x+1)2+$(y-\sqrt{3})^{2}$=1,可得圆心C$(-1,\sqrt{3})$,半径r=1.
点P(-1,0)到圆心C的距离d=$\sqrt{3}$.
A(ρ,θ)化为直角坐标A(x,y).
∴|OA|2+|MA|2=x2+y2+(x+2)2+y2=2[(x+1)2+y2]+2∈[2×3-1+2,2×3+1+2],即|OA|2+|MA|2∈[7,9].
点评 本题考查了极坐标方程与直角坐标方程的互化、点与圆的位置关系、两点之间的距离公式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
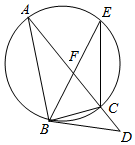 如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${C}_{n}^{m}$=${C}_{n}^{n-m}$ | B. | ${C}_{m}^{m}$+${C}_{m}^{m-1}$=${C}_{m+1}^{m}$ | ||
| C. | ${C}_{5}^{1}$+${C}_{5}^{2}$=${C}_{5}^{3}$ | D. | ${C}_{n+1}^{m}$=${C}_{n}^{m-1}$+${C}_{n-1}^{m}$+${C}_{n-1}^{m-1}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com