
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.分析 (1)设MC,BN交于F,连结EF,由四边形BCNM是平行四边形可得F是BN的中点,由中位线定理得EF∥AN,故AN∥平面MEC;
(2)VE-CMN=$\frac{1}{2}$VA-CMN=$\frac{1}{2}$VC-ANM=$\frac{1}{2}$VB-ANM=$\frac{1}{2}$VN-MAB=$\frac{1}{2}$VD-MAB=$\frac{1}{2}$VM-ABD.
解答 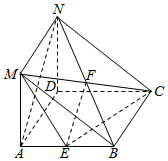 证明:(1)设MC,BN交于F,连结EF,
证明:(1)设MC,BN交于F,连结EF,
∵四边形BCNM是平行四边形,
∴F是BN的中点,∵E是AB的中点,
∴EF∥AN,
又AN?平面MEC,EF?平面MEC,
∴AN∥平面MEC.
(2)∵E是AB的中点,∴VE-CMN=$\frac{1}{2}$VA-CMN=$\frac{1}{2}$VC-ANM.
∵BC∥平面ADNM,∴VC-ANM=VB-ANM=VN-MAB,
∵ND∥平面ABM,∴VN-MAB=VD-MAB=VM-ABD.
∵平面ADNM⊥平面ABCD,平面ADNM∩平面ABCD=AD,MA⊥AD,
∴MA⊥平面ABCD,
∵S△ABD=$\frac{1}{2}AB•AD•sin∠BAD$=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴VM-ABD=$\frac{1}{3}{S}_{△ABD}•AM$=$\frac{1}{3}×\sqrt{3}×1=\frac{\sqrt{3}}{3}$.
∴VE-CMN=$\frac{1}{2}$VM-ABD=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=|sinx| | B. | y=|cosx| | C. | y=sin2x | D. | y=cos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $±\sqrt{2}$ | B. | ±$\frac{\sqrt{21}}{2}$ | C. | ±2$\sqrt{2}$ | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a30,a1 | B. | a1,a30 | C. | a8,a30 | D. | a8,a7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 公务员 | 教师 | 合计 | |
| 同意延迟退休 | 40 | n | 70 |
| 不同意延迟退休 | m | 20 | p |
| 合计 | 50 | 50 | 100 |
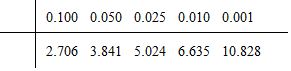
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com